AlegsaOnline.com

Matematika – co to je, hlavní obory a praktické využití

Matematika: co to je, hlavní obory (algebra, geometrie, analýza) a praktické využití v obchodě, vědě, strojírenství a každodenním životě.

Autor: Leandro Alegsa

22-02-2026

Matematika je nauka o číslech, tvarech a vzorcích. Slovo pochází z řeckého slova "μάθημα" (máthema), což znamená "věda, poznání nebo učení", a někdy se zkracuje na maths (v Anglii, Austrálii, Irsku a na Novém Zélandu) nebo math (ve Spojených státech a Kanadě). Tato zkrácená slova studenti a jejich školy často používají pro aritmetiku, geometrii nebo jednoduchou algebru.

Matematika zahrnuje studium:

Čísla: jak lze věci počítat.
Struktura: jak jsou věci uspořádány. Tento podobor se obvykle nazývá algebra.
Místo: místo, kde se věci nacházejí, a jejich uspořádání. Tento podobor se obvykle nazývá geometrie.
Změna: jak se věci mění. Tato podoblast se obvykle nazývá analýza.

Matematika je užitečná při řešení problémů, které se vyskytují v reálném světě, a proto ji kromě matematiků studuje a používá mnoho dalších lidí. V současné době jsou některé matematické znalosti potřebné v mnoha zaměstnáních. Lidé pracující v obchodě, vědě, strojírenství a stavebnictví potřebují určité znalosti matematiky.

Hlavní obory matematiky

Aritmetika – základní operace s čísly (sčítání, odčítání, násobení, dělení), matematika každodenního použití.
Algebra – práce s neznámými, rovnicemi a strukturami (polynomy, grupy, okruhy).
Geometrie – tvar, velikost a vlastnosti prostorových i roviných útvarů.
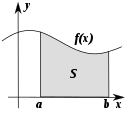
Matematická analýza – zkoumá limity, derivace a integrály; zajišťuje nástroje pro popis změn a průběhů.
Teorie pravděpodobnosti a statistika – práce s náhodou, odhadování parametrů, testování hypotéz a analýza dat.
Diskrétní matematika – kombinatorika, grafy, teorie čísel; důležitá v informatice.
Numerická matematika – algoritmy pro přibližné řešení rovnic a modelů (počítačové výpočty).
Topologie – zkoumá vlastnosti prostorů zachované při plynulých deformacích.
Matematické modelování – přepis reálných situací do matematických rovnic a objektů pro analýzu a simulaci.

Praktické využití matematiky

Matematika je základem mnoha oborů a použití v každodenním životě i v průmyslu:

Věda a technika: navrhování strojů, simulace fyzikálních systémů, zpracování signálů, analýza dat.
Informatika: algoritmy, šifrování a bezpečnost, teorie komplexity, strojové učení a umělá inteligence.
Ekonomie a finance: modelování rizika, výpočet úroků, oceňování finančních nástrojů, optimalizace portfolia.
Stavebnictví a architektura: statika konstrukcí, přesné rozměry a geometrické návrhy.
Medicína a biologie: modelování šíření nemocí, analýza genomických dat, zpracování medicínských snímků.
Doprava a navigace: optimalizace tras, systémové řízení provozu, GPS a geodézie.
Každodenní život: rozpočty, vaření podle receptů, plánování času, vyhodnocení rizik.

Jak matematika pracuje

Matematika staví na několika základních principech a metodách:

Abstrakce – zjednodušení reálných situací na modely, které lze analýzou ověřit.
Důkaz – logické odvození a ověření tvrzení; důslednost a přesnost jsou klíčové.
Výpočty – přesné i numerické postupy pro získání výsledků v praxi.
Vizualizace – grafy, diagramy a geometrické znázornění usnadňují pochopení.
Modelování – tvorba rovnic či algoritmů, které popisují chování systémů.

Krátká historická poznámka

Matematika má kořeny v dávných civilizacích (Babilónie, Egypt) a dále se rozvíjela ve starověkém Řecku. Klíčové milníky zahrnují vznik algebraických postupů, geometrii Euklida, a v novověku kalkulus (Newton, Leibniz). Moderní matematika se rozvětvila do teoretických i aplikovaných disciplín a rychle se rozvíjí s nástupem výpočetní techniky.

Tipy pro učení matematiky

Procvičujte pravidelně příklady – opakování upevňuje pochopení.
Nechte si vysvětlit myšlenky slovy i vizuálně – různé způsoby pomáhají porozumět.
Učte se důkazy krok po kroku, soustřeďte se na logiku argumentu.
Používejte nástroje: kalkulačky, grafické programy, online kurzy a interaktivní simulace.
Provádějte modelování reálných problémů – to propojí teorii s praxí.

Matematika je tedy nejen teoretická disciplína, ale především univerzální nástroj pro analýzu a řešení problémů v mnoha oblastech lidské činnosti. Díky kombinaci logiky, abstrakce a praktických výpočtů má významné uplatnění od školních lavic až po výzkum a průmysl.

Řešení problémů v matematice

Matematika řeší problémy pomocí logiky. Jedním z hlavních nástrojů logiky, které matematici používají, je dedukce. Dedukce je zvláštní způsob myšlení, který umožňuje objevovat a dokazovat nové pravdy pomocí starých pravd. Pro matematika je důvod, proč je něco pravdivé (tzv. důkaz), stejně důležitý jako skutečnost, že je to pravdivé, a tento důvod se často nachází pomocí dedukce. Právě používání dedukce odlišuje matematické myšlení od jiných druhů vědeckého myšlení, které se může opírat o experimenty nebo o rozhovory.

Logiku a uvažování používají matematici k vytváření obecných pravidel, která jsou důležitou součástí matematiky. Tato pravidla vynechávají informace, které nejsou důležité, takže jedno pravidlo může pokrýt mnoho situací. Nalezením obecných pravidel řeší matematika mnoho problémů najednou, protože tato pravidla lze použít i na jiné problémy. Tato pravidla se mohou nazývat teorémy (pokud byla dokázána) nebo domněnky (pokud ještě není známo, zda jsou pravdivá). Většina matematiků používá k nalezení logického důkazu nelogické a kreativní uvažování.

Někdy matematika nachází a studuje pravidla nebo myšlenky, kterým zatím nerozumíme. Často jsou v matematice myšlenky a pravidla vybírány proto, že jsou považovány za jednoduché nebo přehledné. Na druhou stranu někdy jsou tyto myšlenky a pravidla nalezeny v reálném světě až poté, co jsou studovány v matematice; to se v minulosti stalo již mnohokrát. Obecně platí, že studium pravidel a myšlenek matematiky nám může pomoci lépe porozumět světu. Příklady matematických problémů jsou sčítání, odčítání, násobení, dělení, počítání, zlomky a desetinná čísla. Problémy algebry se řeší vyhodnocením určitých proměnných. Kalkulačka odpovídá na každý matematický problém ve čtyřech základních aritmetických operacích.

Oblasti studia matematiky

Číslo

Matematika zahrnuje studium čísel a veličin.Je to vědní obor, který se zabývá logikou tvaru, množství a uspořádání. Většina níže uvedených oblastí se studuje v mnoha různých oborech matematiky, včetně teorie množin a matematické logiky. Studium teorie čísel se obvykle zaměřuje spíše na strukturu a chování celých čísel než na samotné základy čísel, a proto není v této podkapitole uvedeno.

0 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0,125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0,125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Přirozená čísla	Celá čísla	Racionální čísla	Reálná čísla	Komplexní čísla
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} $f(x)={\sqrt {x}}$
Pořadová čísla	Kardinální čísla	Aritmetické operace	Aritmetické vztahy	Funkce

Struktura

Mnoho oblastí matematiky zkoumá strukturu, kterou má objekt. Většina těchto oblastí je součástí studia algebry.


Teorie čísel	Abstraktní algebra	Lineární algebra	Teorie řádu	Teorie grafů

Tvar

Některé oblasti matematiky zkoumají tvary věcí. Většina těchto oblastí je součástí studia geometrie.


Topologie	Geometrie	Trigonometrie	Diferenciální geometrie	Fraktální geometrie

Změna

Některé oblasti matematiky studují způsob, jakým se věci mění. Většina těchto oblastí je součástí studia analýzy.


Calculus	Vektorový výpočet	Analýza

Diferenciální rovnice	Dynamické systémy	Teorie chaosu

Aplikovaná matematika

Aplikovaná matematika využívá matematiku k řešení problémů jiných oblastí, jako je inženýrství, fyzika a výpočetní technika.

Numerická analýza - Optimalizace - Teorie pravděpodobnosti - Statistika - Matematické finance - Teorie her - Matematická fyzika - Dynamika tekutin - Výpočetní algoritmy

Slavné věty

Tyto věty zaujaly matematiky i lidi, kteří matematiky nejsou.

Pythagorova věta - Fermatova poslední věta - Goldbachova domněnka - Domněnka o dvojím prvočísle - Gödelovy věty o neúplnosti - Poincarého domněnka - Cantorův diagonální argument - Věta o čtyřech barvách - Zornovo lemma - Eulerova identita - Churchova-Turingova věta

Jedná se o věty a domněnky, které výrazně změnily matematiku.

Riemannova hypotéza - Hypotéza kontinua - P versus NP - Pythagorova věta - Centrální limitní věta - Základní věta kalkulu - Základní věta algebry - Základní věta aritmetiky - Základní věta projektivní geometrie - Klasifikační věty ploch - Gaussova-Bonnetova věta - Fermatova poslední věta - Kantorova věta

Základy a metody

Pokrok v chápání podstaty matematiky ovlivňuje také způsob, jakým matematici studují svůj předmět.

Filozofie matematiky - Matematický intuicionismus - Matematický konstruktivismus - Základy matematiky - Teorie množin - Symbolická logika - Teorie modelů - Teorie kategorií - Logika - Reverzní matematika - Tabulka matematických symbolů

Historie a svět matematiků

Matematika v dějinách a dějiny matematiky.

Historie matematiky - Časová osa matematiky - Matematici - Fieldsova medaile - Abelova cena - Problémy tisíciletí (Clayovacena zamatematiku) - Mezinárodní matematická unie - Matematické soutěže - Laterální myšlení - Matematika a pohlaví

Ocenění v matematice

Nobelova cena za matematiku se neuděluje. Matematici mohou za významné práce získat Abelovu cenu a Fieldsovu medaili.

Clayův matematický institut prohlásil, že dá milion dolarů tomu, kdo vyřeší jeden z problémů Ceny tisíciletí.

Matematické nástroje

Existuje mnoho nástrojů, které se používají k provádění matematiky nebo k hledání odpovědí na matematické problémy.

Starší nástroje

Abacus
Napierovy kosti, posuvné pravidlo
Pravítko a kompas
Mentální výpočet

Novější nástroje

Kalkulačky a počítače
Programovací jazyky
Systémy počítačové algebry (výpis)
Internetová zkratka
software pro statistickou analýzu (například SPSS)
Programovací jazyk SAS
Programovací jazyk R

Viz také

Časová osa žen v matematice
Americká matematická společnost
Společnost pro průmyslovou a aplikovanou matematiku
Genealogický projekt Matematika
Předmětová klasifikace matematiky

Otázky a odpovědi

Otázka: Co je to matematika?

Odpověď: Matematika je nauka o číslech, tvarech a vzorcích. Slovo pochází z řeckého μάθημα (máthema), což znamená "věda, poznání nebo učení".

Otázka: Jaké jsou hlavní oblasti matematiky?

Odpověď: Mezi hlavní oblasti matematiky patří čísla, struktura (algebra), místo (geometrie) a změna (analýza).

Otázka: Jak se matematika používá v reálném světě?

Odpověď: Aplikovaná matematika je užitečná při řešení problémů v reálném světě. Matematiku používají lidé pracující v obchodě, vědě, strojírenství a stavebnictví.

Otázka: Existuje zkrácená verze slova "matematika"?

Odpověď: Ano - v zemích Britského společenství národů se zkracuje na "maths" a v Severní Americe na "math".

Otázka: Co znamená slovo "matematika"?

Odpověď: Slovo "matematika" pochází z řeckého μάθημα (máthema) a znamená "věda, poznání nebo učení".

Otázka: Jaký typ řešení problémů zahrnuje aplikovaná matematika?

Odpověď: Aplikovaná matematika zahrnuje řešení problémů v reálném světě, s nimiž se setkávají lidé pracující v obchodě, vědě, strojírenství a stavebnictví.