Pythagorova věta (a²+b²=c²): definice, vzorec a důkazy

Pythagorova věta: definice, vzorec a přehled důkazů. Srozumitelný výklad, příklady a postupy pro snadné pochopení a²+b²=c² a praktické výpočty.

Autor: Leandro Alegsa

17-03-2026 13:15

Pythagorova věta je v matematice základní tvrzení o stranách pravoúhlého trojúhelníku.

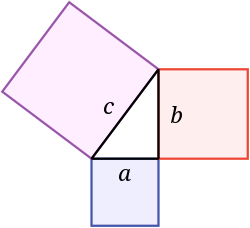
Jeden z úhlů v pravoúhlém trojúhelníku je vždy roven 90 stupňům a tento úhel se nazývá pravý úhel. Dvě strany, které svírají pravý úhel, se běžně nazývají ramena a třetí strana protilehlá pravému úhlu se nazývá přepona (hypotenuse) — vždy jde o nejdelší stranu trojúhelníku. Název věty je odvozen od řeckého matematika Pythagora (Pythagorovi).

Pythagorova věta říká, že plocha čtverce postaveného na přeponě se rovná součtu ploch čtverců postavených na ramenech. Vizuálně je to patrné na klasickém obrázku, kde plocha modrého čtverce plus plocha červeného čtverce dá ploše fialového čtverce. Jsou‑li délky ramen a a b a délka přepony c, pak platí

a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

Existuje mnoho různých důkazů této věty. Dělí se přibližně do několika kategorií:

Geometrické důkazy – přeuspořádáním částí (rearrangement) nebo pomocí ploch.
Důkazy pomocí podobnosti – nejčastěji využívají podobné trojúhelníky v pravoúhlém trojúhelníku a vztahy mezi stranami.
Algebraické a analytické důkazy – využívají souřadnice, rovnici čar a výpočty délek (vzdálenost dvou bodů).
Důkazy pomocí integrálů, vektorů či lineární algebry – moderní přístupy, které větu ukazují z obecnějších hledisek.

Důkaz pomocí podobnosti trojúhelníků (stručně)

V pravoúhlém trojúhelníku ABC s pravým úhlem v C spusťme výšku z C na přeponu AB; vzniknou dva menší trojúhelníky, které jsou podobné celému trojúhelníku. Z podobnosti plyne několik poměrových vztahů, z nichž po úpravě dostaneme a^2 + b^2 = c^2 (kde a a b jsou délky ramen a c délka přepony). Tento důkaz je standardní v učebnicích geometrie díky své jednoduchosti a přehlednosti.

Geometrický důkaz přeuspořádáním

V příkladu s čtverci na stranách se vezme čtverec o straně (a+b) a do něj se umístí čtyři shodné pravoúhlé trojúhelníky tak, že uprostřed vznikne čtverec o straně c. Porovnáním ploch (celková plocha = plocha čtyř trojúhelníků + plocha prostředního čtverce nebo = součet jednotlivých čtverců na stranách) vyjde a^2 + b^2 = c^2.

Algebraický/analytický důkaz

Položme pravoúhlý trojúhelník do souřadnicové soustavy: bod C v počátku (0,0), bod A v (a,0) a bod B v (0,b). Vzdálenost mezi A a B (přepona c) se spočítá pomocí Pythagorovy formule pro vzdálenost dvou bodů: c = sqrt((a-0)^2 + (0-b)^2) = sqrt(a^2 + b^2), což po umocnění dává tytéž vztahy.

Konverz a zobecnění

Konverze: Pokud v trojúhelníku stran splňují a^2 + b^2 = c^2, pak je úhel mezi stranami o délkách a a b pravý — tedy věta má i svoji obrácenou verzi.
Obecnější předpis: Pro libovolný trojúhelník s délkami stran a, b, c a úhlem γ mezi stranami a a b platí zákon kosin: c^2 = a^2 + b^2 − 2ab cos γ; pro γ = 90° (cos γ = 0) získáme Pythagorovu větu.
Vyšší dimenze: V eukleidovských prostorách s metrikou Eukleidovou je délka úhlopříčky obdélníkového paralelogramu nebo vzdálenost mezi body dána obdobnou sumou čtverců souřadnic (obecná Pythagorova relace v n‑dimenzích).

Pythagorejské trojice

Počet celých trojic (a,b,c) splňujících a^2+b^2=c^2 je nekonečný. Základní generační vzorec pro primitivní trojice (tj. takové, kde a, b, c jsou navzájem nesoudělné) je: pro celá kladná m>n platí

a = m^2 − n^2,
b = 2mn,
c = m^2 + n^2.

Příklady: (3,4,5), (5,12,13), (8,15,17).

Praktické aplikace

Výpočet vzdálenosti mezi dvěma body v rovině (základ pro GPS, mapování, počítačovou grafiku).
Konstrukční úlohy v technice a stavebnictví (měření výšek, délek, kontrola pravých úhlů).
Základy trigonometie a analytické geometrie – odvození základních vztahů mezi délkami a úhly.

Příklad

Mějme a = 3, b = 4. Potom a^2 + b^2 = 9 + 16 = 25 = c^2, takže c = 5. Trojúhelník s těmito délkami je pravoúhlý a tvoří známou pythagorejskou trojici (3,4,5).

Pythagorova věta patří mezi nejznámější a nejčastěji používané věty v matematice právě díky své prostotě i všestrannosti; její desítky různých důkazů ukazují, že jde o hloubkově fundamentální vztah mezi geometrií a algebrou.

Důkaz

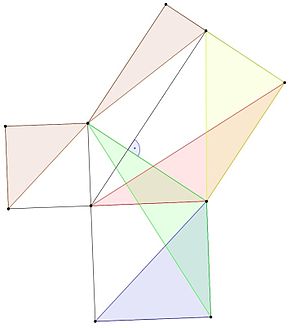
Jeden z důkazů Pythagorovy věty nalezl řecký matematik Eudoxos z Knidu.

Důkaz se opírá o tři lemmata:

Trojúhelníky se stejnou základnou a výškou mají stejnou plochu.
Trojúhelník, který má stejnou základnu a výšku jako strana čtverce, má stejnou plochu jako polovina čtverce.
Trojúhelníky se dvěma shodnými stranami a jedním shodným úhlem jsou shodné a mají stejný obsah.

Důkazem je:

Modrý trojúhelník má stejnou plochu jako zelený trojúhelník, protože má stejnou základnu i výšku (lemma 1).
Zelený i červený trojúhelník mají dvě strany rovné stranám stejných čtverců a úhel rovný přímce (úhel 90 stupňů) plus úhel trojúhelníku, takže jsou shodné a mají stejný obsah (lemma 3).
Plochy červeného a žlutého trojúhelníku jsou stejné, protože mají stejnou výšku i základnu (lemma 1).
Plocha modrého trojúhelníku se rovná ploše žlutého trojúhelníku, protože

A b l u e = A g r e e e n = A r e d = A y e l l o w {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}}. ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Hnědé trojúhelníky mají ze stejných důvodů stejnou plochu.
Modrá a hnědá barva mají každá polovinu plochy menšího čtverce. Součet jejich ploch se rovná polovině plochy většího čtverce. Z tohoto důvodu jsou poloviny ploch malých čtverců stejné jako polovina plochy většího čtverce, takže jejich plochy jsou stejné jako plochy většího čtverce.

Důkaz pomocí podobných trojúhelníků

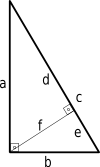
Další důkaz Pythagorovy věty můžeme získat pomocí podobných trojúhelníků.

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

Z obrázku víme, že c = d + e {\displaystyle c=d+e\,\! } $c=d+e\,\!$ . A nahrazením rovnic (1) a (2):

c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

Násobení písmenem c:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!. } $c^{2}=a^{2}+b^{2}\,\!.$

Pythagorovy trojice

Pythagorovy trojice neboli triplety jsou tři celá čísla, která odpovídají rovnici a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

Známým příkladem je trojúhelník o stranách 3, 4 a 5. Jestliže a=3 a b=4, pak 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ , protože 9 + 16 = 25 {\displaystyle 9+16=25} $9+16=25$ . To lze také zobrazit jako 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

Trojúhelník tři-čtyři-pět funguje pro všechny násobky 3, 4 a 5. Jinými slovy, čísla jako 6, 8, 10 nebo 30, 40 a 50 jsou také pythagorejskými trojicemi. Dalším příkladem trojúhelníku je trojúhelník 12-5-13, protože 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}}=13} ${\sqrt {12^{2}+5^{2}}}=13$ .

Pythagorova trojice, která není násobkem jiných trojic, se nazývá primitivní pythagorovská trojice. Každou primitivní pythagorovskou trojici lze najít pomocí výrazu ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})}. $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , ale musí být splněny následující podmínky. Ty kladou omezení na hodnoty m {\displaystyle m} a n {\displaystyle n} .

m {\displaystyle m} a n {\displaystyle n} jsou kladná celá čísla
m {\displaystyle m} a n {\displaystyle n} nemají žádné společné činitele kromě 1
m {\displaystyle m} a n {\displaystyle n} mají opačnou paritu. m {\displaystyle m} a n {\displaystyle n} mají opačnou paritu, když m {\displaystyle m} je sudé a n {\displaystyle n} je liché, nebo m {\displaystyle m} je liché a n {\displaystyle n} je sudé.
m > n {\displaystyle m>n} .

Jsou-li splněny všechny čtyři podmínky, pak hodnoty m {\displaystyle m} a n {\displaystyle n} tvoří primitivní pythagorejskou trojici.

m = 2 {\displaystyle m=2} $m=2$ a n = 1 {\displaystyle n=1} $n=1$ tvoří primitivní pythagorovskou trojici. Hodnoty splňují všechny čtyři podmínky. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\krát 2\krát 1=4}. $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ a m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5}. $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , takže vznikne trojice ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ .

Otázky a odpovědi

Otázka: Co je to Pythagorova věta?

Odpověď: Pythagorova věta je tvrzení o stranách pravoúhlého trojúhelníku.

Otázka: Jaký úhel je v pravoúhlém trojúhelníku vždy roven 90 stupňům?

Odpověď: Jeden z úhlů pravoúhlého trojúhelníku je vždy roven 90 stupňům, což se označuje jako pravý úhel.

Otázka: Jak se nazývají dvě strany vedle pravého úhlu?

Odpověď: Dvě strany vedle pravého úhlu se nazývají rameny.

Otázka: Jak se nazývá strana ležící naproti pravému úhlu?

Odpověď: Strana ležící naproti pravému úhlu se nazývá přepona a je to vždy nejdelší strana.

Otázka: Existuje rovnice pro výpočet této věty?

Odpověď: Ano, existuje rovnice pro výpočet této věty, která říká, že "čtverec délky přepony se rovná součtu čtverců délek ostatních dvou stran".

Otázka: Jsou všechny trojúhelníky s úhlem 90 stupňů považovány za "pravoúhlé" trojúhelníky?

Odpověď: Ne, ne všechny trojúhelníky s úhlem 90 stupňů jsou považovány za "pravoúhlé" trojúhelníky; za "pravoúhlé" lze považovat pouze ty, u nichž je jedna strana (přepona) delší než ostatní dvě strany a na svém konci svírá úhel 90 stupňů.

Vyhledávání