Trigonometrie

Trigonometrie (z řeckého trigonon = tři úhly a metron = míra) je část základní matematiky zabývající se úhly, trojúhelníky a trigonometrickými funkcemi, jako je sinus (zkráceně sin), kosinus (zkráceně cos) a tangens (zkráceně tan). Má určitou souvislost s geometrií, i když se neshodneme na tom, jaká přesně je tato souvislost; pro některé je trigonometrie jen částí geometrie.

Přehled a definice

V trigonometrii se pro popis částí trojúhelníku používá velké množství specifických slov. Některé z definic v trigonometrii jsou:

Pravoúhlý trojúhelník - Pravoúhlý trojúhelník je trojúhelník, jehož úhel je roven 90°. (Trojúhelník nemůže mít více než jeden pravý úhel) Standardní trigonometrické poměry lze použít pouze pro pravoúhlé trojúhelníky.
Hypotenuse - Hypotenuse trojúhelníku je nejdelší strana a strana, která je protilehlá pravému úhlu. Například pro trojúhelník vpravo je přeponou strana c.
Protilehlá strana úhlu - Protilehlá strana úhlu je strana, která se neprotíná s vrcholem úhlu. Například strana a je opakem úhlu A v trojúhelníku vpravo.
Přilehlá strana úhlu - Přilehlá strana úhlu je strana, která protíná vrchol úhlu, ale není jeho přeponou. Například strana b sousedí s úhlem A v trojúhelníku vpravo.

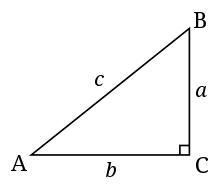
Standardní pravoúhlý trojúhelník. C je pravý úhel na tomto obrázku

Trigonometrické poměry

Existují tři hlavní trigonometrické poměry pro pravoúhlé trojúhelníky a tři reciproké poměry těchto poměrů. Celkem je 6 poměrů. Jsou to:

Sinus (sin) - Sinus úhlu se rovná opačné hypotezule {\displaystyle {{\text{Opposite}} \over {\text{Hypotenuse}}}} ${{\text{Opposite}} \over {\text{Hypotenuse}}}$
Kosinus (cos) - Kosinus úhlu se rovná přilehlé hypotezule {\displaystyle {{\text{Přilehlá}} \over {\text{Hypotenuse}}}} ${{\text{Adjacent}} \over {\text{Hypotenuse}}}$
Tangens (tan) - Tangens úhlu se rovná opačnému sousednímu {\displaystyle {{\text{Opposite}}. \over {\text{Přilehlý}}}} ${{\text{Opposite}} \over {\text{Adjacent}}}$

Reciproční hodnoty těchto poměrů jsou:

Kosekant (csc) - Kosekant úhlu se rovná Hypotenuse Opačný {\displaystyle {{\text{Hypotenuse}} \over {\text{Opposite}}}} ${{\text{Hypotenuse}} \over {\text{Opposite}}}$ nebo csc θ = 1 sin θ {\displaystyle \csc \theta ={1 \over \sin \theta }}}. $\csc \theta ={1 \over \sin \theta }$

Sekant (sec) - Sekant úhlu se rovná Hypotenuse Přilehlé {\displaystyle {{\text{Hypotenuse}} \over {\text{Adjacent}}}} ${{\text{Hypotenuse}} \over {\text{Adjacent}}}$ nebo sec θ = 1 cos θ {\displaystyle \sec \theta ={1 \over \cos \theta }}}. $\sec \theta ={1 \over \cos \theta }$

Kotangens (cot) - Kotangens úhlu se rovná přilehlému protilehlému {\displaystyle {{\text{Přilehlý}}. \over {\text{Opposite}}}} ${{\text{Adjacent}} \over {\text{Opposite}}}$ nebo cot θ = 1 tan θ {\displaystyle \cot \theta ={1 \over \tan \theta }}}. $\cot \theta ={1 \over \tan \theta }$

Studenti často používají mnemotechnickou pomůcku, aby si tento vztah zapamatovali. Poměry sinus, kosinus a tangens v pravoúhlém trojúhelníku si lze zapamatovat tak, že si je představíme jako řetězce písmen, například SOH-CAH-TOA:

Sinus = protilehlý ÷ hypotezula

Kosinus = sousední ÷ Hypotenuse

Tangens = protilehlý ÷ sousední

Použití trigonometrie

Pomocí sinusů a kosinusů lze zodpovědět prakticky všechny otázky týkající se trojúhelníků. Tomu se říká "řešení" trojúhelníku. Zbývající úhly a strany libovolného trojúhelníku lze vypočítat, jakmile jsou známy dvě strany a jejich zahrnutý úhel nebo dva úhly a strana nebo tři strany. Tyto zákony jsou užitečné ve všech odvětvích geometrie, protože každý mnohoúhelník lze popsat jako kombinaci trojúhelníků.

Trigonometrie je také důležitá v geodézii, ve vektorové analýze a při studiu periodických funkcí.

Existuje také sférická trigonometrie, která se zabývá sférickou geometrií. Ta se používá pro výpočty v astronomii, geodézii a navigaci.

Zákony trigonometrie

Sinusový zákon

a Sin A = b Sin B = c Sin C {\displaystyle {{\text{a}} \over {\text{Sin A}}={{\text{b}} \over {\text{Sin B}}={{\text{c}} \over {\text{Sin C}}}} ${{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}$

Kosinův zákon

a 2 = b 2 + c 2 - 2 b c cos ( A ) {\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(A)} $a^{2}=b^{2}+c^{2}-2bc\cos(A)$

Zákon tangenty

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ) {\displaystyle {\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}}. ${\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}$