Trigonometrická funkce
V matematice jsou trigonometrické funkce souborem funkcí, které vztahují úhly ke stranám pravoúhlého trojúhelníku. Existuje mnoho trigonometrických funkcí, tři nejčastější jsou sinus, kosinus a tangens, dále pak kotangens, sekant a kosekant. Poslední tři se nazývají reciproční trigonometrické funkce, protože se chovají jako reciproké funkce jiných funkcí. Sekant a kosekant se používají zřídka.
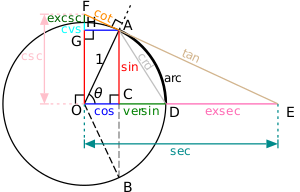
Všechny trigonometrické funkce libovolného úhlu lze sestrojit pomocí kružnice se středem v bodě O o poloměru 1.

Trigonometrické funkce: sinus , kosinus , tangens , kosekant , sekant , kotangens .
Definice
Trigonometrické funkce se někdy nazývají také kruhové funkce. Jsou to funkce úhlu, které jsou důležité mimo jiné při studiu trojúhelníků. Trigonometrické funkce se běžně definují jako poměry dvou stran pravoúhlého trojúhelníku obsahujícího daný úhel, ekvivalentně je lze definovat jako délky různých úseček z jednotkové kružnice (kružnice, která má poloměr jedna).
Definice pravoúhlého trojúhelníku
Chcete-li definovat trigonometrické funkce pro úhel A, začněte s pravoúhlým trojúhelníkem, který obsahuje úhel A:
Pro strany trojúhelníku používáme následující názvy:
- Přepona je strana protilehlá pravému úhlu nebo definovaná jako nejdelší strana pravoúhlého trojúhelníku, v tomto případě h.
- Protilehlá strana je strana opačná k úhlu, který nás zajímá, v tomto případě a.
- Přilehlá strana je strana, která se dotýká úhlu, který nás zajímá, a pravý úhel, odtud její název. V tomto případě je sousední stranou strana b.
Všechny trojúhelníky jsou v euklidovské geometrii chápány tak, že součet vnitřních úhlů každého trojúhelníku je π radiánů (neboli 180°); pro pravoúhlý trojúhelník jsou tedy dva nepravoúhlé úhly v rozmezí nula až π/2 radiánů. Čtenář by si měl uvědomit, že následující definice striktně vzato definují trigonometrické funkce pouze pro úhly v tomto rozsahu. Rozšíříme je na celou množinu reálných argumentů pomocí jednotkové kružnice nebo požadavkem určitých symetrií a požadavkem, aby šlo o periodické funkce.
1) Sinus úhlu je poměr délky protější strany k délce přepony. V našem případě
sin A = protilehlá přepona = a h . {\displaystyle \sin A={\frac {\textrm {opozitní}}{\textrm {hypotenuse}}}={\frac {a}{h}}. }
Všimněte si, že tento poměr nezávisí na konkrétním zvoleném pravoúhlém trojúhelníku, pokud obsahuje úhel A, protože všechny tyto trojúhelníky jsou si podobné.
Množina nul sinusu (tj. hodnot x {\displaystyle x}

{ n π | n ∈ Z } . {\displaystyle \levice\{n\pi {\big |}n\in \mathbb {Z} \vpravo\}. }
2) Kosinus úhlu je poměr délky přilehlé strany k délce přepony. V našem případě
cos A = sousední přepona = b h . {\displaystyle \cos A={\frac {\textrm {přilehlá}}{\textrm {hypotenuse}}}={\frac {b}{h}}. }
Množina nul kosinu je
{ π 2 + n π | n ∈ Z } . {\displaystyle \levice\{{\frac {\pi }{2}}+n\pi {\bigg |}n\in \mathbb {Z} \vpravo\}. }
3) Tangens úhlu je poměr délky protější strany k délce strany sousední. V našem případě
tan A = opačný sousední = a b . {\displaystyle \tan A={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {a}{b}}. }
Množina nul tečny je
{ n π | n ∈ Z } . {\displaystyle \levice\{n\pi {\big |}n\in \mathbb {Z} \vpravo\}. }
Stejná množina funkce sinus od
tan A = sin A cos A . {\displaystyle \tan A={\frac {\sin A}{\cos A}}. }
Zbývající tři funkce lze nejlépe definovat pomocí výše uvedených tří funkcí.
4) Kosekant csc(A) je multiplikativní inverzní hodnota sin(A), tj. poměr délky přepony k délce protější strany:
csc A = hypotenuse opposite = h a {\displaystyle \csc A={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}}
5) Sekant sec(A) je multiplikativní inverzní hodnota cos(A), tj. poměr délky přepony k délce sousední strany:
sec A = hypotenuse adjacent = h b {\displaystyle \sec A={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}={\frac {h}{b}}}
6) Kotangens cot(A) je multiplikativní inverzní hodnota tan(A), tj. poměr délky sousední strany k délce strany protilehlé:
cot A = sousední opačný = b a {\displaystyle \cot A={\frac {\textrm {sousední}}{\textrm {opačný}}}={\frac {b}{a}}}
Definice pomocí mocninných řad
Trigonometrické funkce lze definovat také pomocí mocninných řad:
sin x = x - x 3 3 ! + x 5 5 ! - x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}
cos x = 1 - x 2 2 ! + x 4 4 ! - x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n ( 2 n ) ! {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
a definujte tečnu, kotangens, sekant a kosekant pomocí identit, viz níže.
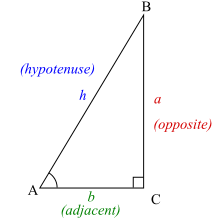
Pravoúhlý trojúhelník vždy obsahuje úhel 90° (π/2 radiánů), zde označený C. Úhly A a B se mohou lišit. Trigonometrické funkce určují vztahy mezi délkami stran a vnitřními úhly pravoúhlého trojúhelníku.
Identity
Některé důležité identity:
tan x = sin x cos x {\displaystyle \tan x={\frac {\sin x}{\cos x}}}
cot x = cos x sin x {\displaystyle \cot x={\frac {\cos x}{\sin x}}}
sec x = 1 cos x {\displaystyle \sec x={\frac {1}{\cos x}}}
csc x = 1 sin x {\displaystyle \csc x={\frac {1}{\sin x}}}
sin 2 x + cos 2 x = 1 {\displaystyle \sin ^{2}x+\cos ^{2}x=1}
sin 2 x = 2 sin x cos x {\displaystyle \sin 2x=2\sin x\cos x}
cos 2 x = cos x cos x - sin x sin x = cos 2 x - sin 2 x = 2 cos 2 x - 1 = 1 - 2 sin 2 x {\displaystyle \cos 2x=\cos x\cos x-\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x}
tan 2 x = 2 tan x 1 - tan 2 x {\displaystyle \tan 2x={\frac {2\tan x}{1-\tan ^{2}x}}}
sin ( x ± y ) = sin x cos y ± cos x sin y {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y}
cos ( x ± y ) = cos x cos y ∓ sin x sin y {\displaystyle \cos \left(x\pm y\right)=\cos x\cos y\mp \sin x\sin y}
tan ( x ± y ) = tan x ± tan y 1 ∓ tan x tan y {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}} 
Hyperbolické funkce
Hyperbolické funkce mají velmi podobné vlastnosti jako trigonometrické funkce. Jsou definovány pomocí exponenciální funkce, která vychází z konstanty e.
- Hyperbolický sinus:
sinh x = e x - e - x 2 = e 2 x - 1 2 e x = 1 - e - 2 x 2 e - x . {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}. }
- Hyperbolický kosinus:
cosh x = e x + e - x 2 = e 2 x + 1 2 e x = 1 + e - 2 x 2 e - x . {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}. }
- Hyperbolický tangens:
tanh x = sinh x cosh x = e x - e - x e x + e - x = e 2 x - 1 e 2 x + 1 = 1 - e - 2 x 1 + e - 2 x . {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}={\frac {1-e^{-2x}}{1+e^{-2x}}}. }
- Hyperbolický kotangens:
coth x = cosh x sinh x = e x + e - x e x - e - x = e 2 x + 1 e 2 x - 1 = 1 + e - 2 x 1 - e - 2 x , x ≠ 0. {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}={\frac {1+e^{-2x}}{1-e^{-2x}}},\qquad x\neq 0.}
- Hyperbolický sekant:
sech x = 1 cosh x = 2 e x + e - x = 2 e x e 2 x + 1 = 2 e - x 1 + e - 2 x . {\displaystyle \operatorname {sech} \,x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}={\frac {2e^{-x}}{1+e^{-2x}}}. }
- Hyperbolický kosekant:
csch x = 1 sinh x = 2 e x - e - x = 2 e x e 2 x - 1 = 2 e - x 1 - e - 2 x , x ≠ 0. {\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}={\frac {2e^{-x}}{1-e^{-2x}}},\qquad x\neq 0.} 
Související stránky
Vyhledávání






















