Funkce (matematika)
V matematice je funkce matematický objekt, který po zadání vstupu vytváří výstup - může to být číslo, vektor nebo cokoli, co může existovat uvnitř množiny věcí.
Funkce je tedy něco jako stroj, který přijímá hodnoty x a vrací výstup y. Množina všech hodnot, které může x nabývat, se nazývá doména. Množina, která obsahuje všechny hodnoty, které může nabývat y, se nazývá doména.
Pokud se tak stane, říkáme, že y je funkce x, a píšeme y =f(x). f je název funkce a píše se f : X → Y {\displaystyle f:X\to Y}. 
(funkce z X do Y), abychom znázornili tři části funkce: obor (x), spoluobor (y) a párovací proces (šipka).
Příkladem funkce je f(x)=x+1. Jako vstup zadáme přirozené číslo x {\displaystyle x}
(0,1,2,3...) a získáme přirozené číslo y {\displaystyle y}. 
což je x {\displaystyle x} +1 (1,2,3,4...) Myšlenka funkce byla vytvořena tak, aby pokryla všechny druhy možností. Funkce nemusí být rovnice. Hlavní myšlenkou je, že vstupy a výstupy jsou nějak spárovány, i když je proces velmi složitý.
Metafory
Tabulky
Vstupy a výstupy lze zapsat do tabulky jako na obrázku; to je snadné, pokud není dat příliš mnoho.
Grafy
Na obrázku je vidět, že 2 i 3 byly spárovány s c; v opačném směru to není dovoleno, 2 nemohla vyvést c a d,každý vstup může mít pouze jeden výstup. Všechny f ( x ) {\displayystyle f(x)} 
(c a d na obrázku) se obvykle nazývají obrazová množina f {\displaystyle f}
a obrazová množina může být celá kodoména nebo ne. Lze říci, že podmnožina A kodoménu s obrazovou množinou je f(A). Pokud mají vstupy a výstupy nějaké pořadí, je snadné je zakreslit do grafu: Tímto 
způsobem obraz přijde na obraz množiny A. Tím se oba 2 a 3 mají spárovány s není dovoleno v opačném směru, i jeden může dělat mezi codomain nebo ne. Lze učinit závěr, že podmnožina A kodoménu je obrazem množiny je F(A).
Historie
V 90. letech 16. století použili GottfriedLeibniz a Johann Bernoulli slovo funkce v písmenech mezi sebou, takže moderní pojem vznikl ve stejné době jako kalkulus.
V roce 1748 Leonhard Euler uvedl: "V roce 1755 pak: "Závisí-li některé veličiny na jiných veličinách natolik, že změní-li se tyto veličiny, změní se i ty první, pak se první veličiny nazývají funkcemi těch druhých. Tato definice platí poměrně široce a zahrnuje všechny způsoby, jimiž může být jedna veličina určena jinou. Označuje-li tedy x proměnnou veličinu, pak se všechny veličiny, které na x nějakým způsobem závisí nebo jsou jím určeny, nazývají funkce x." Což je velmi moderní.
Obvykle se Dirichletovi připisuje verze používaná ve školách až do druhé poloviny 20. století: Je také jedno, jakým způsobem je tato korespondence vytvořena." (D. Dirichlet): "y je funkcí proměnné x, definovanou na intervalu a < x < b, jestliže každé hodnotě proměnné x v tomto intervalu odpovídá určitá hodnota proměnné y."
V roce 1939 Bourbaki Dirichletovu definici zobecnil a podal její množinově teoretickou verzi jako korespondenci mezi vstupy a výstupy; ta se ve školách používala přibližně od roku 1960.
Nakonec v roce 1970 Bourbaki uvedl moderní definici jako trojici f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} 
, přičemž F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\podmnožina X\časů Y,(x,f(x))\v F}
(tj. f : X → Y {\displaystyle f:X\do Y} a F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } {\displaystyle F=\{(x,f(x))|x\v X,f(x)\v Y\}} 
).
Typy funkcí
- Základní funkce - funkce, které se obvykle učí ve škole: zlomky, odmocniny, funkce sinus, kosinus a tangens a některé další funkce.
- Nezákladní funkce - Většina z nich nepoužívá operace, které se neučíme ve škole (jako + nebo - nebo mocniny). Mnoho integrálů je neelementárních.
- Inverzní funkce - Funkce, které ruší jinou funkci. Například: je-li F(x) inverzní funkce k f(x)=y, pak F(y)=x. Ne všechny funkce mají inverzní funkce.
- Speciální funkce: Funkce, které mají názvy. Například: sinus, kosinus a tangens. Funkce jako f(x)=3x (třikrát x) se nenazývají speciální funkce. Mohou být elementární, neelementární nebo inverzní.
Otázky a odpovědi
Otázka: Co je v matematice funkce?
Odpověď: Funkce v matematice je objekt, který po zadání vstupu, jímž může být číslo, vektor nebo cokoli, co může existovat uvnitř množiny věcí, vytváří výstup.
Otázka: Jaké dvě množiny jsou spojeny s funkcemi?
Odpověď: Množina všech hodnot, které může nabývat x, se nazývá doména a množina, která obsahuje všechny hodnoty, které může nabývat y, se nazývá spoludoména.
Otázka: Jak se funkce často označují?
Odpověď: Funkce se často označují kurzivou, například f, g, h.
Otázka: Jak funkci znázorňujeme?
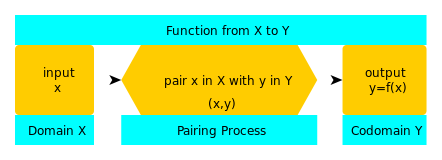
Odpověď: Funkci znázorňujeme zápisem y = f(x), kde f je název funkce a píše se f : X → Y (funkce z X do Y), čímž se znázorňují tři části funkce - doména (X), kodoména (Y) a párovací proces (šipka).
Otázka: Můžete uvést příklad funkce?
Odpověď: Příkladem funkce je f(x) = x + 1. Jako vstup zadáme přirozené číslo x a dostaneme přirozené číslo y, které je x + 1. Například zadáme-li jako vstup do funkce f číslo 3, dostaneme na výstupu číslo 4.
Otázka: Musí být každá funkce rovnicí?
Odpověď: Ne, ne každá funkce musí být rovnicí. Hlavní myšlenkou funkcí je, že vstupy a výstupy jsou nějakým způsobem spárovány - i když to může být velmi složité.
