Sada

Zápis

Většina matematiků používá při psaní o množinách velká písmena (obvykle latinku). Věci, které jsou považovány za prvky množin, se obvykle píší malými římskými písmeny.

Jedním ze způsobů zobrazení množiny je seznam jejích členů oddělených čárkami a uzavřených do závorek. Například,

• X={1,2,3} je množina, která má členy 1, 2 a 3.

Jiným způsobem je vyjádření toho, co platí o členech množiny, například takto:

• {x | x je přirozené číslo & x < 4}.

Tedy v mluvené angličtině: "množina všech x takových, že x je přirozené číslo a x je menší než čtyři".

Prázdná množina se zapisuje zvláštním způsobem:

• ∅ {\\displaystyle \emptyset }

Pokud je objekt a členem množiny A, zapisuje se jako:

• a ∈ A.

Tedy v mluvené angličtině: "a je členem A"

Co dělat se sadami

Prvek

Do sáčku lze vložit různé věci. Později by bylo vhodné se zeptat, zda je v tašce určitá věc. Matematici tento prvek nazývají. Něco je prvkem množiny, pokud se tato věc nachází v příslušném pytli. Symbol, který se pro to používá, je ∈ {\displaystyle \in }.

a ∈ A {\displaystyle a\in \mathbf {A} }

znamená, že a {\displaystyle a} je v sáčku A {\displaystyle \mathbf {A} }

Prázdná sada

Stejně jako taška může být i sada prázdná. Prázdná množina je jako prázdný pytel: nejsou v ní žádné věci.

Porovnávání sad

Lze porovnat dvě sady. Je to jako dívat se na dvě různé tašky. Pokud obsahují stejné věci, jsou si rovny.

Kardinalita množiny

Když matematici mluví o množině, chtějí někdy vědět, jak je množina velká. Dělají to tak, že spočítají, kolik prvků je v množině (kolik položek je v pytli). Kardinalita může být jednoduché číslo. Prázdná množina má kardinalitu 0. Množina { a p l e , o r a n g e }. {\displaystyle \{jablko,pomeranč\}} má kardinalitu 2.

Dvě množiny mají stejnou kardinalitu, pokud můžeme jejich prvky spárovat - pokud můžeme spojit dva prvky, jeden z každé množiny. Množina { a p l e , o r a n g e } {\displaystyle \{jablko,pomeranč}} a množina { s u n , m o o n } {\displaystyle \{sun,moon\}} mají stejnou kardinalitu. Jablko můžeme spojit se sluncem a pomeranč s měsícem. Na pořadí nezáleží. Prvky je možné spárovat a žádný není vynechán. Ale množina { d o g , c a t , b i r d } {\displaystyle \{pes,kočka,pták\}} a množina {5 , 6 }. {\displaystyle \{5,6\}} mají různou kardinalitu. Pokud se je pokusíme spárovat, vždy jedno zvíře vynecháme.

Nekonečná kardinalita

Někdy kardinalita není číslo. Někdy má množina nekonečnou kardinalitu. Množina celých čísel je množina s nekonečnou kardinalitou. Některé množiny s nekonečnou kardinalitou jsou větší (mají větší kardinalitu) než jiné. Například reálných čísel je více než přirozených čísel. To znamená, že množinu celých čísel a množinu reálných čísel nemůžeme spárovat, ani kdybychom pracovali donekonečna. Pokud má množina stejnou kardinalitu jako množina celých čísel, nazývá se spočetná množina. Má-li však množina stejnou kardinalitu jako množina reálných čísel, nazývá se nepočetná množina.

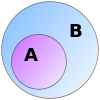
Podsady

Pokud se podíváte na množinu {a,b} a množinu {a,b,c,d}, zjistíte, že všechny prvky první množiny jsou také v druhé množině.
 Říkáme: {a,b} je podmnožinou {a,b,c,d}.
 Jako vzorec to vypadá takto:
{ a , b } ⊆ { a , b , c , d } {\displaystyle \{a,b\}\subseteq \{a,b,c,d\}}

Pokud jsou všechny prvky A zároveň prvky B, nazýváme A podmnožinou B:
A ⊆ B {\displaystyle A\subseteq B}
 Obvykle se čte "A je obsaženo v B".

Příklad:
Každý Chevrolet je americké auto. Množina všech Chevroletů je tedy obsažena v množině všech amerických automobilů.

Nastavené operace

Sady lze kombinovat různými způsoby.

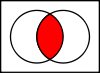
Křižovatky

Průnik A ∩ B {\displaystyle A\cap B} dvou množin A a B je množina, která obsahuje všechny prvky,
které jsou jak v množině A, tak v množině B.
Je-li A množina všech levných aut a B množina všech amerických aut,
pak A ∩ B {\displaystyle A\cap B} je množina všech levných amerických aut.

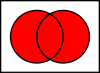
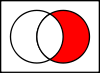
Odbory

Sjednocení A ∪ B {\displaystyle A\cup B} dvou množin A a B je množina, která obsahuje všechny prvky, které jsou v
množině A nebo v množině B.

Toto "nebo" je inkluzivní disjunkce, takže sjednocení obsahuje i prvky, které jsou v množině A a v množině B.

Mimochodem: To znamená, že průnik je podmnožinou sjednocení:

( A ∩ B ) ⊆ ( A ∪ B ) {\displaystyle (A\cap B)\subseteq (A\cup B)}

Je-li A množina všech levných aut a B množina všech amerických aut,
pak A ∪ B {\displaystyle A\cup B} je množina všech aut bez všech drahých aut, která nejsou z Ameriky.

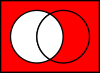
Doplňky

Doplněk může znamenat dvě různé věci:

• Doplněk A je vesmír U bez všech prvků A:

A C = U ∖ A {\displaystyle A^{\rm {C}}=U\setminus A}
 Vesmír U je množina všech věcí, o kterých mluvíte.
Je-li U množina všech aut a A množina všech levných aut,
pak A^C je množina všech drahých aut.

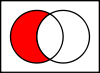
• Relativní doplněk A v B je množina B bez všech prvků A:

B ∖ A {\displaystyle B\setminus A}
 Často se nazývá rozdíl množin.
Je-li A množina všech levných automobilů a B množina všech amerických automobilů,
pak B ∖ A {\displaystyle B\setminus A} je množina všech drahých amerických automobilů.

Vyměníte-li množiny v rozdílu množin, výsledek je jiný:
V příkladu s auty je rozdíl A ∖ B {\displaystyle A\setminus B} množinou všech levných aut, která nejsou vyrobena v Americe.

             

Speciální sady

Některé množiny jsou pro matematiku velmi důležité. Používají se velmi často. Jednou z nich je prázdná množina. Mnohé z těchto množin se zapisují tučným písmem na tabuli, jak je uvedeno níže. Mezi speciální množiny patří např:

• P {\displaystyle \mathbb {P} } , označující množinu všech prvočísel.
• N {\displaystyle \mathbb {N} } , označující množinu všech přirozených čísel. To znamená, že N {\displaystyle \mathbb {N} } = {1, 2, 3, ...}, nebo někdy N {\displaystyle \mathbb {N} } = {0, 1, 2, 3, ...}.
• Z {\displaystyle \mathbb {Z} } , označující množinu všech celých čísel (kladných, záporných nebo nulových). Z {\displaystyle \mathbb {Z} je tedy celé číslo. } = {..., -2, -1, 0, 1, 2, ...}.
• Q {\displaystyle \mathbb {Q} } , označující množinu všech racionálních čísel (tj. množinu všech vlastních a nevlastních zlomků). Q = { a b : a , b ∈ Z , b ≠ 0 }. {\displaystyle \mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}\end{matrix}}:a,b\in \mathbb {Z} ,b\neq 0\right\}} , což znamená všechny zlomky a b {\displaystyle {\begin{matrix}{\frac {a}{b}}\end{matrix}} kde a a b jsou v množině všech celých čísel a b není rovno 0. Například 1 4 ∈ Q {\displaystyle {\begin{matrix}{\frac {1}{4}}\end{matrix}}}v \mathbb {Q} } a 11 6 ∈ Q {\displaystyle {\begin{matrix}{\frac {11}{6}}\end{matrix}}\in \mathbb {Q} } . V této množině jsou všechna celá čísla, protože každé celé číslo a lze vyjádřit jako zlomek a 1 {\displaystyle {\begin{matrix}{\frac {a}{1}}\end{matrix}}} .
• R {\displaystyle \mathbb {R} } , označující množinu všech reálných čísel. Tato množina zahrnuje všechna racionální čísla spolu se všemi iracionálními čísly (tj. čísly, která nelze přepsat jako zlomky, jako jsou π , {\displaystyle \pi ,} e , {\displaystyle e,} a √2).
• C {\displaystyle \mathbb {C} } , označující množinu všech komplexních čísel.

Každá z těchto množin čísel má nekonečný počet prvků a P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C {\displaystyle \mathbb {P} \subset \mathbb {N} \podskupina \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} } . Prvočísla se mimo teorii čísel a příbuzné obory používají méně často než ostatní.

 

Paradoxy o množinách

Matematik Bertrand Russell zjistil, že s touto teorií množin jsou problémy. Uvedl to v paradoxu zvaném Russellův paradox. Snadněji pochopitelná verze, bližší reálnému životu, se nazývá Barberův paradox:

Paradox holiče

Někde je malé městečko. V tom městečku je holič. Všichni muži v městečku nemají rádi vousy, a tak se buď holí sami, nebo chodí do holičství, aby je holič oholil.

Můžeme tedy učinit prohlášení o samotném holiči: Holič holí všechny muže, kteří se neholí sami. Holí pouze tyto muže (protože ostatní se holí sami a nepotřebují holiče, aby je oholil).

To samozřejmě vyvolává otázku: Co dělá holič každé ráno, aby vypadal čistě oholený? To je paradox.

• Pokud se holič sám neoholí, bude se řídit pravidlem a oholí se sám (půjde se oholit do holičství).
• Pokud se holič skutečně oholí sám, neoholí se podle výše uvedeného pravidla.