Teorie grafů
Teorie grafů je obor matematiky týkající se grafů. Graf je abstraktní zobrazení: řady bodů, které jsou spojeny přímkami. Každý bod se obvykle nazývá vrchol (více než jeden se nazývá vrcholy) a čáry se nazývají hrany. Grafy jsou nástrojem pro modelování vztahů. Používají se k hledání odpovědí na řadu problémů.
Některé z těchto otázek jsou:
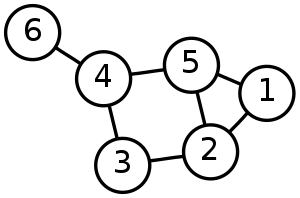
Neorientovaný graf.
Různé druhy grafů
- Teorie grafů má mnoho aspektů. Grafy mohou být směrované nebo neusměrněné. Příkladem směrovaného grafu může být systém silnic ve městě. Některé ulice ve městě jsou jednosměrné. To znamená, že na těchto úsecích lze jet pouze jedním směrem.
- Grafy mohou být vážené. Příkladem může být silniční síť se vzdálenostmi nebo s mýtným (pro silnice).
- Uzly (kolečka na obrázku) grafu se nazývají vrcholy. Čáry spojující vrcholy se nazývají hrany. Mezi dvěma uzly nemusí být žádná čára, může být jedna čára nebo může být více čar.
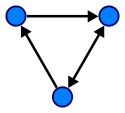
Směrovaný graf.
Historie
 →
→ →
→ 
Vizualizace sedmi mostů na Königbergu. Tento problém vyřešil Leonhard Euler v roce 1736, což vedlo k rozvoji topologie a moderní teorie grafů.
Graf je abstraktní datová struktura. Obsahuje uzly, které spolu obvykle souvisejí. Uzel je soubor dat, obvykle ve formě uspořádaných dvojic. Uzly jsou buď propojeny, nebo nejsou propojeny s jiným uzlem. Vztah mezi uzly je obvykle definován jako hrana (Edge). Grafy jsou užitečné pro svou schopnost spojovat uzly s jinými uzly. V praxi existuje několik reprezentací Grafů.
Leonhard Euler žil ve městě zvaném Königsberg. (Jeho název se v roce 1946 změnil na Kaliningrad). Město leží na řece Pregel. Na řece se nachází ostrov. Přes řeku vede několik mostů. Euler chtěl každý z mostů obejít a jednou použít. Zeptal se, zda to může udělat. V roce 1736 publikoval vědecký článek, kde ukázal, že to není možné. Dnes je tento problém známý jako Sedm mostů v Königsbergu. Článek je považován za první článek v historii teorie grafů.
Tento článek, stejně jako článek, který napsal Vandermonde o problému rytíře, pokračoval v analýze situs, kterou zahájil Leibniz. Eulerův vzorec o počtu hran, vrcholů a stěn konvexního mnohostěnu studovali a zobecnili Cauchy a L'Huillier a stojí u zrodu topologie.
Spojení myšlenek pocházejících z matematiky s myšlenkami pocházejícími z chemie stojí u zrodu části standardní terminologie teorie grafů. Konkrétně termín "graf" zavedl Sylvester v článku publikovaném v roce 1878 v časopise Nature.
Jedním z nejznámějších a nejproduktivnějších problémů teorie grafů je problém čtyř barev: "Je pravda, že každá mapa nakreslená v rovině může mít své oblasti obarvené čtyřmi barvami tak, že libovolné dvě oblasti se společnou hranicí mají různé barvy?".
.png)
Problém Königsberg Bridge na mapě města
.png)
Stejný problém, ale s použitím grafu
Teorie grafů v perspektivě
Teorie grafů je důležitou součástí matematiky a informatiky. Pro mnoho takových problémů existují přesná řešení. Mnohdy je však velmi obtížné je vypočítat. Proto se velmi často používají aproximace. Existují dva druhy takových aproximací, Monte-Carlo algoritmy a Las-Vegas algoritmy.
Otázky a odpovědi
Otázka: Co je to teorie grafů?
Odpověď: Teorie grafů je obor matematiky, který se zabývá studiem grafů, což jsou abstraktní zobrazení bodů spojených přímkami.
Otázka: Jak se nazývají body v grafu?
Odpověď: Body v grafu se obvykle označují jako vrcholy.
Otázka: Co představují čáry mezi vrcholy?
Odpověď: Čáry mezi vrcholy představují vztahy nebo spojení mezi nimi.
Otázka: Jak lze grafy používat?
Odpověď: Grafy lze použít k modelování vztahů a hledání odpovědí na různé problémy.
Otázka: Jaké otázky mohou grafy pomoci zodpovědět?
Odpověď: Grafy mohou pomoci odpovědět na otázky týkající se analýzy sítí, optimalizace a plánování.
Otázka: Existují různé typy grafů?
Odpověď: Ano, existují různé typy grafů, například směrové a neusměrněné grafy, vážené a nevážné grafy, úplné a neúplné grafy atd.
Otázka: Existuje nějaký software pro práci s teorií grafů?
Odpověď: Ano, existuje software pro práci s teorií grafů, například Gephi a NetworkX.
Vyhledávání