Problém čtyř barev
Věta o čtyřech barvách je matematická věta. Říká, že na libovolné rovinné ploše s oblastmi (lidé si je představují jako mapy) mohou být oblasti obarveny nejvýše čtyřmi barvami. Dvě oblasti, které mají společnou hranici, nesmí dostat stejnou barvu. Nazývají se sousední (vedle sebe), pokud mají společnou úsečku hranice, nikoliv jen bod.
Jednalo se o první větu, která byla dokázána počítačem, a to důkazem vyčerpáním. Při důkazu vyčerpáním se závěr stanoví tak, že se rozdělí na případy a každý z nich se dokazuje zvlášť. Případů může být mnoho. Například první důkaz věty o čtyřech barvách byl důkaz vyčerpáním s 1 936 případy. Tento důkaz byl kontroverzní, protože většina případů byla ověřena počítačovým programem, nikoliv ručně. Nejkratší dnes známý důkaz věty o čtyřech barvách má stále více než 600 případů.
Přestože byl tento problém poprvé představen jako problém pro kolorování politických map zemí, tvůrci map se o něj příliš nezajímají. Podle článku historika matematiky Kennetha Maye (Wilson 2002, 2): "Mapy využívající pouze čtyři barvy jsou vzácné a ty, které je využívají, obvykle vyžadují pouze tři. Knihy o kartografii a historii tvorby map se o vlastnosti čtyř barev nezmiňují".
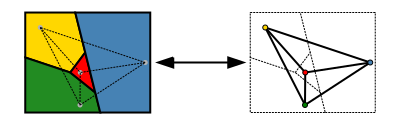
Mnoho jednodušších map lze vybarvit třemi barvami. Čtvrtá barva je nutná u některých map, například u těch, kde je jedna oblast obklopena lichým počtem dalších, které se navzájem cyklicky dotýkají. Jeden takový příklad je uveden na obrázku. Věta o pěti barvách říká, že k vybarvení mapy stačí pět barev. Má krátký, elementární důkaz a byla dokázána na konci 19. století. (Heawood 1890) Důkaz, že stačí čtyři barvy, se ukázal být mnohem obtížnější. Od prvního výroku věty o čtyřech barvách v roce 1852 se objevilo mnoho falešných důkazů a falešných protipříkladů.

Příklad čtyřbarevné mapy

Tři barvy na vybarvení této mapy nestačí.
Přesná formulace problému
Intuitivně lze větu o čtyřech barvách vyjádřit takto: "Při jakémkoli rozdělení roviny na sousedící oblasti, které se nazývá mapa, lze tyto oblasti vybarvit nejvýše čtyřmi barvami tak, aby žádné dvě sousedící oblasti neměly stejnou barvu. Abychom mohli problém správně vyřešit, je třeba objasnit některé aspekty: Zaprvé je třeba ignorovat všechny body, které patří třem nebo více zemím. Za druhé, bizarní mapy s oblastmi o konečné ploše a nekonečném obvodu mohou vyžadovat více než čtyři barvy.
Pro účely věty musí být každá "země" jednoduše spojenou oblastí nebo souvislou oblastí. Ve skutečném světě to však neplatí: Aljaška jako součást Spojených států, Nachčivan jako součást Ázerbájdžánu a Kaliningrad jako součást Ruska nejsou spojité. Protože území určitého státu musí mít stejnou barvu, nemusí čtyři barvy stačit. Vezměme si například zjednodušenou mapu, jako je ta na obrázku vlevo: Na této mapě patří dva regiony označené A ke stejné zemi a musí mít stejnou barvu. Tato mapa pak vyžaduje pět barev, protože dva regiony A spolu sousedí se čtyřmi dalšími regiony, z nichž každý sousedí se všemi ostatními. Pokud by region A měl pouze tři regiony, mohlo by být potřeba šest nebo více barev. Tímto způsobem je možné vytvořit mapy, které potřebují libovolně vysoký počet barev. Podobná konstrukce platí i v případě, že se pro všechny vodní plochy použije jediná barva, jak je to obvyklé na skutečných mapách.
Jednodušší verze věty využívá teorii grafů. Množinu oblastí mapy lze abstraktněji znázornit jako neorientovaný graf, který má vrchol pro každou oblast a hranu pro každou dvojici oblastí, které mají společnou hraniční úsečku. Tento graf je rovinný: lze jej nakreslit v rovině bez křížení umístěním každého vrcholu na libovolně zvolené místo v rámci regionu, kterému odpovídá, a nakreslením hran jako křivek, které vedou bez křížení v rámci každého regionu z místa vrcholu do každého společného hraničního bodu regionu. Tímto způsobem lze naopak z mapy vytvořit libovolný rovinný graf. V grafově-teoretické terminologii věta o čtyřech barvách říká, že vrcholy každého planárního grafu lze obarvit nejvýše čtyřmi barvami tak, aby žádné dva sousední vrcholy neměly stejnou barvu, nebo zkráceně "každý planární graf je čtyřbarevný" (Thomas 1998, s. 849; Wilson 2002).

Příklad mapy Ázerbájdžánu s nesouvislými regiony

Tuto mapu nelze vybarvit čtyřmi barvami.
Historie
První, kdo tento problém pojmenoval, byl Francis Guthrie v roce 1852. V té době byl studentem práv v Anglii. Zjistil, že k vybarvení mapy hrabství Anglie potřebuje nejméně čtyři barvy. Poprvé se problémem zabýval Augustus de Morgan v dopise, který napsal Rowanu Hamlitonovi v srpnu 1852. V dopise se de Morgan ptá, zda čtyři barvy skutečně stačí k vybarvení mapy tak, aby země, které jsou vedle sebe, dostaly různé barvy.
Anglický matematik Arthur Cayley předložil tento problém matematické společnosti v Londýně v roce 1878. Do roka Alfred Kempe našel něco, co vypadalo jako důkaz problému. O jedenáct let později, v roce 1890, Percy Heawood ukázal, že Alfredův důkaz je chybný. Peter Guthrie Tait předložil další pokus o důkaz v roce 1880. Trvalo jedenáct let, než se ukázalo, že ani Taitův důkaz nefunguje. V roce 1891 to mohl dokázat Julius Petersen. Když falzifikoval Cayleyho důkaz, ukázal Kempe také důkaz pro problém, který nazval věta o pěti barvách. Věta říká, že každou takovou mapu lze obarvit nejvýše pěti barvami. Existují dvě omezení: Za prvé, každá země je přilehlá, neexistují žádné exklávy. Druhé omezení spočívá v tom, že země musí mít společnou hranici; pokud se dotýkají pouze v jednom bodě, lze je vybarvit stejnou barvou. I když byl Kempeho důkaz chybný, použil některé myšlenky, které později umožnily správný důkaz.
V 60. a 70. letech 20. století vytvořil Heinrich Heesch první náčrt důkazu pomocí počítače. Kenneth Appel a Wolfgang Haken tento náčrt v roce 1976 vylepšili (Robertson et al. 1996). Podařilo se jim snížit počet případů, které by bylo třeba otestovat, na 1936; později vznikla verze, která počítala s testováním pouze 1476 případů. Každý případ musel být testován počítačem (Appel & Haken 1977).
V roce 1996 Neil Robertson, Daniel Sanders, Paul Seymour a Robin Thomas tuto metodu vylepšili a snížili počet testovaných případů na 663. Opět bylo nutné každý případ testovat pomocí počítače.
V roce 2005 Georges Gonthier a Benjamin Werner vypracovali formální důkaz. To bylo zlepšení, protože to poprvé umožnilo použít software pro dokazování teorémů. Použitý software se nazývá Coq.
Věta o čtyřech barvách je prvním velkým matematickým problémem, který byl dokázán pomocí počítače. Protože důkaz nemůže provést člověk, někteří matematici jej neuznali za správný. Pro ověření důkazu je nutné spoléhat na správně fungující software a hardware, který důkaz ověří. Protože důkaz byl proveden pomocí počítače, není také příliš elegantní.
Pokusy, které se ukázaly jako chybné
Věta o čtyřech barvách je známá tím, že ve své dlouhé historii přitahovala velké množství falešných důkazů a vyvrácení. Deník The New York Times nejprve odmítl o Appelově-Hakenově důkazu informovat. Noviny tak učinily v rámci své politiky; obávaly se, že důkaz se ukáže jako nepravdivý stejně jako ty předchozí (Wilson 2002, s. 209). U některých důkazů trvalo dlouho, než se je podařilo zfalšovat: V případě Kempeho a Taitových důkazů trvalo jejich falšování více než deset let.
Nejjednodušší protipříklady se obvykle snaží vytvořit jednu oblast, která se dotýká všech ostatních. To nutí zbývající oblasti vybarvit pouze třemi barvami. Protože platí věta o čtyřech barvách, je to vždy možné; protože se však osoba kreslící mapu soustředí na jednu velkou oblast, nevšimne si, že zbývající oblasti lze ve skutečnosti vybarvit třemi barvami.
Tento trik lze zobecnit: Pokud jsou barvy některých oblastí v mapě zvoleny předem, není možné zbývající oblasti vybarvit tak, aby byly použity celkem pouze čtyři barvy. Někoho, kdo ověřuje protipříklad, nemusí napadnout, že může být potřeba změnit barvu těchto oblastí. Protipříklad tak bude vypadat jako platný, i když tomu tak není.
Jedním z důsledků, který je základem tohoto běžného mylného názoru, je možná skutečnost, že omezení barvy není tranzitivní: oblast musí být zbarvena jinak pouze v oblastech, kterých se přímo dotýká, nikoli v oblastech, které se dotýkají oblastí, kterých se dotýká. Pokud by toto omezení platilo, rovinné grafy by vyžadovaly libovolně velký počet barev.
Jiné falešné důkazy porušují předpoklady věty neočekávaným způsobem, například použitím oblasti, která má více nespojitých částí, nebo tím, že se oblasti stejné barvy nemohou dotýkat v jednom bodě.
Vybarvení politických map
V reálném životě má mnoho zemí exklávy nebo kolonie. Protože patří k dané zemi, je třeba je vybarvit stejnou barvou jako mateřskou zemi. To znamená, že k vybarvení takové mapy je obvykle potřeba více než čtyři barvy. Když matematici hovoří o grafu spojeném s tímto problémem, říkají, že není rovinný. I když je snadné ověřit, zda je graf planární, najít nejmenší počet barev potřebných k jeho vybarvení je velmi obtížné. Je NP-úplný, což je jeden z nejobtížnějších problémů, které existují. Nejmenší počet barev potřebných k obarvení grafu se nazývá jeho chromatické číslo. Mnoho problémů, které se vyskytují při snaze vyřešit větu o čtyřech barvách, souvisí s diskrétní matematikou. Z tohoto důvodu se často používají metody z algebraické topologie.
Rozšíření na "neploché" mapy
Věta o čtyřech barvách vyžaduje, aby se "mapa" nacházela na rovné ploše, kterou matematici nazývají rovina. V roce 1890 Percy John Heawood vytvořil to, čemu se dnes říká Heawoodova domněnka: Ta si klade stejnou otázku jako věta o čtyřech barvách, ale pro libovolný topologický objekt. Jako příklad lze uvést torus, který lze obarvit nejvýše sedmi barvami. Heawoodova domněnka dává vzorec, který funguje pro všechny takové objekty s výjimkou Kleinovy láhve.
Otázky a odpovědi
Otázka: Co je to věta o čtyřech barvách?
Odpověď: Věta o čtyřech barvách je matematická věta, která říká, že na libovolné rovinné ploše s oblastmi lze oblasti vybarvit nejvýše čtyřmi barvami. Sousední oblasti nesmí mít stejnou barvu.
Otázka: Jak vznikl první důkaz věty o čtyřech barvách?
Odpověď: První důkaz věty o čtyřech barvách byl důkaz vyčerpáním s 1936 případy. To znamená, že byla stanovena rozdělením na případy a důkazem každého z nich zvlášť.
Otázka: Zajímá tento problém kartografy?
Odpověď: Ne, tvůrci map se o tento problém příliš nezajímají, protože mapy využívající pouze čtyři barvy jsou vzácné a obvykle vyžadují pouze tři barvy. V knihách o kartografii a historii tvorby map se o vlastnosti čtyř barev nepíše.
Otázka: Co je věta o pěti barvách?
Odpověď: Věta o pěti barvách tvrdí, že k vybarvení mapy stačí pět barev, a má krátký, elementární důkaz, který byl dokázán koncem 19. století.
Otázka: Jak obtížné bylo dokázat, že k obarvení mapy stačí pouze čtyři barvy?
Odpověď: Ukázalo se, že dokázat, že k obarvení map jsou potřeba pouze 4 barvy, je mnohem obtížnější, než se očekávalo, protože od prvního tvrzení v roce 1852 se objevilo mnoho falešných důkazů a falešných protipříkladů.
Otázka: Existuje příklad mapy, kde by bylo ke správnému vybarvení všech oblastí potřeba 5 nebo více barev?
Odpověď: Ano, jedním z takových příkladů je situace, kdy je jeden region obklopen lichým počtem dalších, které se vzájemně dotýkají v cyklu - v tomto případě může být ke správnému vybarvení všech regionů potřeba 5 nebo více barev.
Vyhledávání

