Barvení grafů
Barvení grafů je název pro řadu problémů z teorie grafů. Tyto problémy se zabývají barvením (nebo označováním) vrcholů grafu za určitých podmínek. Jednoduchý problém v tomto kontextu může hledat minimální počet barev potřebných k obarvení vrcholů, pokud dva spojené vrcholy nemohou mít stejnou barvu. V zobrazeném grafu se kruhy nazývají vrcholy a čáry, které je spojují, se nazývají hrany. Minimální počet barev potřebných k obarvení grafu se nazývá jeho chromatické číslo.
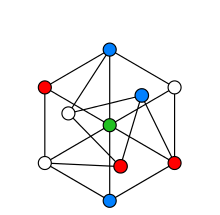
Platné řešení barvení grafu, kdy dva spojené vrcholy nesmí mít stejnou barvu.
Otázky a odpovědi
Otázka: Co je to barvení grafů?
Odpověď: Barvení grafů je problém z teorie grafů, který zahrnuje barvení nebo označování vrcholů grafu podle určitých podmínek.
Otázka: Co je v kontextu barvení grafů jednoduchý problém?
A: Jednoduchý problém může zahrnovat nalezení minimálního počtu barev potřebných k obarvení vrcholů grafu, přičemž je třeba zajistit, aby dva spojené vrcholy neměly stejnou barvu.
Otázka: Jak se nazývají kružnice v grafu?
Odpověď: Kruhy v grafu se nazývají vrcholy.
Otázka: Jak se nazývají čáry spojující kruhy v grafu?
Odpověď: Čáry spojující kruhy v grafu se nazývají hrany.
Otázka: Jak se nazývá minimální počet barev potřebných k vybarvení grafu?
Odpověď: Minimální počet barev potřebných k obarvení grafu se nazývá jeho chromatické číslo.
Otázka: K čemu slouží barvení grafů?
Odpověď: Účelem barvení grafů je najít řešení problémů v teorii grafů, které zahrnují obarvení nebo označení vrcholů grafu podle určitých podmínek.
Otázka: Proč je barvení grafů důležité?
Odpověď: Barvení grafů je důležité v řadě oborů, včetně informatiky, fyziky a společenských věd, a lze je použít k modelování reálných problémů, jako je plánování, přidělování zdrojů a optimalizace sítí.
Vyhledávání