Algebra

Historie

Rané formy algebry vytvořili Babyloňané a řečtí geometři, například Hérós Alexandrijský. Slovo "algebra" je však latinskou podobou arabského slova Al-Džabr ("lití") a pochází z matematické knihy Al-Maqala fi Hisab-al Džabr wa-al-Muqabilah ("Esej o výpočtu lití a rovnice"), kterou v 9. století napsal perský matematik Muhammad ibn Músá al-Chwárizmí, muslim narozený v Chvarizmu v Uzbekistánu. V letech 813-833 n. l. vzkvétal za vlády Al-Ma'mouna v iráckém Bagdádu a zemřel kolem roku 840 n. l. Do Evropy se kniha dostala a byla přeložena do latiny ve 12. století. Kniha pak dostala název "Algebra". (Koncovka matematikova jména al-Chwarizmi byla změněna na slovo, které se v latině lépe vyslovuje, a stalo se z něj anglické slovo algorithm).

Příklady

Zde je jednoduchý příklad algebraického problému:

Sue má 12 bonbónů a Ann má 24 bonbónů. Rozhodnou se, že se rozdělí, aby měly stejný počet bonbonů. Kolik bonbonů bude mít každá z nich?

Pro vyřešení problému můžete použít tyto kroky:

1. Aby měla stejný počet bonbónů, musí Ann dát nějaké Sue. Nechť x představuje počet bonbonů, které Ann dá Sue.
2. Sueiny bonbóny plus x musí být stejné jako Anniny bonbóny minus x. To se zapíše jako: 12 + x = 24 - x
3. Od obou stran rovnice odečtěte 12. Tím získáme: x = 12 - x. (Co se stane na jedné straně rovnítka, musí se stát i na druhé straně, aby rovnice stále platila. V tomto případě tedy po odečtení 12 od obou stran došlo k prostřednímu kroku 12 + x - 12 = 24 - x - 12. V tomto případě se tedy jedná o rovnici, která se skládá ze dvou stran. Poté, co se s tím člověk vyrovná, se prostřední krok nezapisuje).
4. K oběma stranám rovnice přičtěte x. Tím získáme: 2x = 12
5. Obě strany rovnice vydělte číslem 2. Tím získáte x = 6. Odpověď je šest. Pokud Ann dá Sue 6 bonbónů, budou mít stejný počet bonbónů.
6. Chcete-li si to ověřit, dosaďte 6 zpět do původní rovnice, kde bylo x: 12 + 6 = 24 - 6
7. To dává 18=18, což je pravda. Každý z nich má nyní 18 bonbónů.

S praxí lze algebru použít, když se setkáte s problémem, který je příliš obtížný na to, abyste ho vyřešili jiným způsobem. Problémy, jako je stavba dálnice, konstrukce mobilního telefonu nebo nalezení léku na nemoc, vyžadují algebru.

Psaní algebry

Stejně jako ve většině částí matematiky se sčítání z s y (nebo y plus z) zapisuje jako y + z. Odečítání z od y (nebo y minus z) se zapisuje jako y - z. Dělení y z (nebo y nad z: y z {\displaystyle y \nad z} ) se zapisuje jako y ÷ z nebo y/z. častěji se používá y/z.

V algebře lze násobení y číslem z (nebo y krát z) zapsat čtyřmi způsoby: y × z, y * z, y-z nebo jen yz. Symbol násobení "×" se obvykle nepoužívá, protože se příliš podobá písmenu x, které se často používá jako proměnná. Také při násobení většího výrazu lze použít závorky: y (z+1).

Když v algebře násobíme číslo a písmeno, píšeme před písmeno číslo: 5 × y = 5y. Když je číslo 1, pak se jednička nepíše, protože 1 krát libovolné číslo je toto číslo (1 × y = y), a proto není potřeba.

Poznámka na okraj: v algebře nemusíte používat písmena x nebo y. Proměnné jsou pouze symboly, které označují nějaké neznámé číslo nebo hodnotu, takže můžete použít jakoukoli proměnnou. x a y jsou však nejčastější.

Funkce a grafy

Důležitou součástí algebry je studium funkcí, protože funkce se často objevují v rovnicích, které se snažíme řešit. Funkce je jako stroj, do kterého můžete vložit číslo (nebo čísla) a získat z něj určité číslo (nebo čísla). Při používání funkcí nám mohou být grafy mocným nástrojem, který nám pomůže studovat řešení rovnic.

Graf je obrázek, na kterém jsou zobrazeny všechny hodnoty proměnných, díky nimž rovnice nebo nerovnice platí. Obvykle je to snadné, pokud se jedná pouze o jednu nebo dvě proměnné. Grafem je často přímka, a pokud se přímka neohýbá nebo nejde rovně nahoru a dolů, lze ji popsat základním vzorcem y = mx + b. Proměnná b je průsečík grafu y (místo, kde přímka protíná svislou osu) a m je sklon nebo strmost přímky. Tento vzorec platí pro souřadnice grafu, kde každý bod na přímce je zapsán (x, y).

V některých matematických úlohách, jako je rovnice přímky, může být více proměnných (v tomto případě x a y). Pro nalezení bodů na přímce se jedna proměnná změní. Proměnná, která se mění, se nazývá "nezávislá" proměnná. Poté se provede matematický výpočet, aby vzniklo číslo. Číslo, které vznikne, se nazývá "závislá" proměnná. Nezávislá proměnná se většinou zapisuje jako x a závislá proměnná jako y, například v případě y = 3x + 1. To se často zakresluje do grafu pomocí osy x (směřující doleva a doprava) a osy y (směřující nahoru a dolů). Lze ji také zapsat ve tvaru funkce: f(x) = 3x + 1. V tomto příkladu bychom tedy mohli za x dosadit 5 a získat y = 16. Pokud bychom za x dosadili 2, dostali bychom y = 7. A vložením 0 za x bychom dostali y=1. Bodem (5,16), (2,7) a (0,1) by tedy procházela přímka, jak je vidět na grafu vpravo.

Má-li x mocninu 1, je to přímka. Pokud je čtvercem nebo jinou mocninou, je zakřivená. Pokud používá nerovnost (< nebo > ), pak je obvykle část grafu stínovaná, a to buď nad přímkou, nebo pod ní.

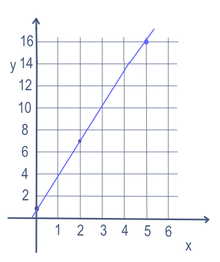
Lineární rovnice pro y=3x+1

Pravidla algebry

V algebře existuje několik pravidel, která lze použít pro další pochopení rovnic. Tato pravidla se nazývají pravidla algebry. Ačkoli se tato pravidla mohou zdát nesmyslná nebo samozřejmá, je moudré si uvědomit, že tyto vlastnosti neplatí ve všech odvětvích matematiky. Proto bude užitečné vědět, jak jsou tato axiomatická pravidla deklarována, než je začneme považovat za samozřejmost. Než přejdeme k samotným pravidlům, zamysleme se nad dvěma definicemi, které budou uvedeny.

1. Opak - opakem {\displaystyle a} je - a {\displaystyle -a}.
2. Reciproční - reciproká hodnota a {\displaystyle a} je 1 a {\displaystyle {\frac {1}{a}}}. .

Pravidla

Komutativní vlastnost sčítání

"Komutativní" znamená, že funkce má stejný výsledek, pokud se čísla prohodí. Jinými slovy, na pořadí členů v rovnici nezáleží. Pokud je operátorem dvou členů sčítání, platí "komutativní vlastnost sčítání". V algebraickém vyjádření to znamená, že a + b = b + a {\displayystyle a+b=b+a} .

Všimněte si, že to neplatí pro odčítání! (tj. a - b ≠ b - a {\displaystyle a-b\neq b-a} )

Komutativní vlastnost násobení

Pokud je operátorem dvou členů násobení, platí "komutativní vlastnost násobení". V algebraickém vyjádření to znamená a ⋅ b = b ⋅ a {\displayystyle a\cdot b=b\cdot a} .

Upozorňujeme, že toto neplatí pro dělení! (tj. a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}}). když a ≠ b {\displaystyle a\neq b} ).

Asociativní vlastnost sčítání

"Asociativní" se vztahuje na seskupení čísel. Asociativní vlastnost sčítání znamená, že při sčítání tří a více členů nezáleží na tom, jak jsou tyto členy seskupeny. Algebraicky to znamená a + ( b + c ) = ( a + b ) + c {\displayystyle a+(b+c)=(a+b)+c} . Všimněte si, že toto neplatí pro odčítání, např. 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} (viz distributivní vlastnost).

Asociativní vlastnost násobení

Z asociativní vlastnosti násobení vyplývá, že při násobení tří a více členů nezáleží na tom, jak jsou tyto členy seskupeny. Algebraicky to znamená a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Všimněte si, že to neplatí pro dělení, např. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Distributivní vlastnost

Distributivní vlastnost říká, že násobení čísla jiným členem lze rozložit. Například: a ⋅ ( b + c ) = a b + a c {\displayystyle a\cdot (b+c)=ab+ac} . (Nezaměňujte to s asociativními vlastnostmi! Například a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .)

Vlastnost aditivní identity

"Identita" označuje vlastnost čísla, že se rovná samo sobě. Jinými slovy, existuje operace dvou čísel tak, že se rovná proměnné součtu. Vlastnost aditivní identity říká, že součet libovolného čísla a 0 je toto číslo: a + 0 = a {\displayystyle a+0=a} . To platí i pro odčítání: a - 0 = a {\displaystyle a-0=a} .

Vlastnost multiplikativní identity

Vlastnost multiplikativní identity říká, že součin libovolného čísla a 1 je toto číslo: a ⋅ 1 = a {\displayystyle a\cdot 1=a} . To platí i pro dělení: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Aditivní inverzní vlastnost

Vlastnost aditivní inverze je něco jako opak vlastnosti aditivní identity. Pokud je operace součtem čísla a jeho opaku a rovná se 0, je tato operace platnou algebraickou operací. Algebraicky to znamená následující: a - a = 0 {\displayystyle a-a=0} . Aditivní inverzní číslo k 1 je (-1).

Multiplikativní inverzní vlastnost

Multiplikativní inverzní vlastnost znamená, že pokud je operace součinem čísla a jeho reciproké hodnoty a je rovna 1, je tato operace platnou algebraickou operací. Algebraicky to znamená: a a = 1 {\displayystyle {\frac {a}{a}}=1} . Multiplikativní inverzní hodnota 2 je 1/2.

Pokročilá algebra

Kromě "elementární algebry" neboli základní algebry existují pokročilé formy algebry, které se vyučují na vysokých školách a univerzitách, jako je abstraktní algebra, lineární algebra a univerzální algebra. Patří sem i to, jak používat matice k řešení mnoha lineárních rovnic najednou. Abstraktní algebra se zabývá věcmi, které se nacházejí v rovnicích, a jde nad rámec čísel k abstraktnějším věcem se skupinami čísel.

Mnoho matematických úloh se týká fyziky a techniky. V mnoha z těchto fyzikálních úloh je proměnnou čas. Čas používá písmeno t. Použití základních myšlenek algebry může pomoci zredukovat matematický problém do nejjednodušší podoby a usnadnit tak řešení obtížných problémů. Energie je e, síla je f, hmotnost je m, zrychlení je a a rychlost světla je někdy c. Toho se využívá v některých známých rovnicích, jako je f = ma a e=mc^2 (i když k vyřešení poslední rovnice bylo zapotřebí složitější matematiky nad rámec algebry).

Související stránky

• Seznam témat matematiky
• Pořadí operací
• Parabola
• Systém počítačové algebry