Elementární algebra
Elementární algebra je nejzákladnější formou algebry, kterou se studenti učí. Často je to jedna z dalších oblastí matematiky, které se studenti učí po aritmetice. Zatímco v aritmetice se vyskytují pouze čísla a operátory jako +, -, × a ÷, v algebře se pro čísla používají proměnné (jako a, x, y). To je užitečné, protože:
- Umožňuje lidem řešit problémy týkající se "neznámých" čísel. To znamená, že se učí o rovnicích a jejich řešení (například "najděte číslo x, kde 3 x + 1 = 10 {\displayystyle 3x+1=10}
").
- Umožňuje zobecnit pravidla z aritmetiky. Zatímco někteří studenti chápou, že 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}.
, pomáhá dokázat, že a + b = b + a {\displaystyle a+b=b+a}
pro všechna a a b. Díky tomu je algebra dobrým krokem k učení se abstrakci (učení se obecným myšlenkám z mnoha příkladů).
- Pomáhá lidem pochopit a vytvořit funkční vztahy (někdy také nazývané příčina a následek). Příkladem může být věta "pokud se prodá x vstupenek, pak bude zisk 3 x - 10 {\displaystyle 3x-10}
dolarů".
Tyto tři okruhy jsou hlavními směry elementární algebry. Elementární algebra se často používá v mnoha dalších předmětech, jako je věda, obchod a stavebnictví. Abstraktní algebra, mnohem pokročilejší téma, se obvykle vyučuje až na konci studia.
Jednoduché úlohy z algebry
Pokud má rovnice pouze jedno neznámé číslo, je někdy snadné ji vyřešit. Neznámé číslo se nazývá "x":
2 x + 4 = 12. {\displaystyle 2x+4=12.\,}
Při řešení jednoduché rovnice s jednou neznámou sčítejte, odčítejte, násobte nebo dělte obě strany rovnice stejným číslem tak, aby neznámá x byla na jedné straně rovnice. Jakmile je x samo o sobě na jedné straně, použijte aritmetiku k určení částky na druhé straně rovnice. Například odečtením čísla 4 od obou stran výše uvedené rovnice:
2 x + 4 - 4 = 12 - 4 {\displayyle 2x+4-4=12-4\,}
získání:
2 x = 8 {\displaystyle 2x=8\,}
Vydělte obě strany číslem 2:
2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}\,}
získání:
x = 4. {\displaystyle x=4.\,}
Možná vám pomůže představit si tuto rovnici jako houpačku nebo rovnováhu - co uděláte na jedné straně, musíte udělat na druhé a vaším hlavním cílem je získat x samo o sobě.
Definice
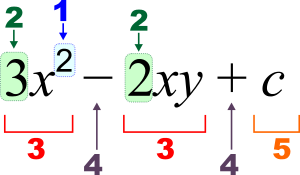
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c}
1 : Exponent (mocnina), 2 : Koeficient, 3 : člen, 4 : operátor, 5 : konstanta, x , y {\displaystyle x,y} : 
Otázky a odpovědi
Otázka: Co je to elementární algebra?
Odpověď: Elementární algebra je nejzákladnější forma algebry, která se učí studenti. Obvykle navazuje na aritmetiku a zahrnuje používání proměnných (jako a, x, y) pro označení čísel v rovnicích.
Otázka: Jaké je využití elementární algebry?
Odpověď: Elementární algebru lze použít k řešení problémů týkajících se neznámých čísel, k zobecnění pravidel z aritmetiky, k pochopení a vytváření funkčních vztahů a často se používá v mnoha dalších předmětech, jako je věda, obchod a stavebnictví.
Otázka: Jak elementární algebra pomáhá lidem pochopit abstraktní myšlenky?
Odpověď: Elementární algebra pomáhá lidem naučit se obecné myšlenky na mnoha příkladech tím, že dokazuje, že a+b=b+a pro všechna a a b. To jim umožňuje lépe porozumět abstraktním pojmům.
Otázka: Je abstraktní algebra pokročilejší než elementární algebra?
Odpověď: Ano, abstraktní algebra se obvykle vyučuje až na konci studia a je mnohem pokročilejší než základní algebra.
Otázka: Jaké typy rovnic zahrnuje elementární algebra?
Odpověď: Elementární algebra zahrnuje rovnice s proměnnými (jako a, x, y), které označují čísla, a operátory jako +,- ,× a ÷ .
3x+1=10 {\displayystyle 3x+1=10}
Otázka: Jak může porozumění elementární algebře pomoci v jiných předmětech?
Odpověď: Porozumění elementární algebře může pomoci v jiných předmětech, jako je věda, obchod nebo stavebnictví, protože umožňuje řešit problémy týkající se neznámých čísel a vytvářet funkční vztahy mezi různými proměnnými.
Vyhledávání




