Násobení
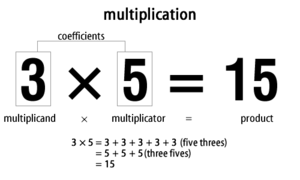
Násobení je aritmetická operace pro zjištění součinu dvou čísel. Násobení je v matematice třetí operací po sčítání, které je první, odčítání, které je druhé, a pak je tu násobení.
U přirozených čísel vám řekne počet dlaždic v obdélníku, kde jedno ze dvou čísel odpovídá počtu dlaždic na jedné straně a druhé číslo odpovídá počtu dlaždic na druhé straně.
Pomocí reálných čísel vám řekne plochu obdélníku, kde první číslo je rovno velikosti jedné strany a druhé číslo je rovno velikosti druhé strany.
Například tři vynásobené pěti je součet pěti trojek nebo součet tří pětek. To lze zapsat jako 3 × 5 = 15 nebo vyslovit jako "tři krát pět je patnáct". Matematici nazývají dvě čísla, která chcete vynásobit, společně "koeficienty" nebo zvlášť "násobek" a "násobitel". Násobek × násobitel = součin.
O násobení čísel se říká, že je komutativní - když pořadí čísel nemá vliv na hodnotu součinu. To platí pro celá čísla (celá čísla), např. 4 × 6 je totéž jako 6 × 4, a také pro racionální čísla (zlomky) a pro všechna ostatní reálná čísla (reprezentovatelná jako pole v spojité čáře) a také pro komplexní čísla (čísla reprezentovatelná jako pole v rovině). Neplatí to pro kvaterniony (čísla reprezentovatelná jako kruh ve čtyřrozměrném prostoru), vektory ani matice.
Definice násobení jako opakovaného sčítání poskytuje způsob, jak dospět k množinově-teoretické interpretaci násobení kardinálních čísel. Přesnější představou je uvažovat o něm jako o škálování veličin. Tato animace znázorňuje násobení čísla 3 číslem 2, jehož výsledkem je číslo 6. Všimněte si, že modrá tečka v modré úsečce délky 3 je umístěna na pozici 1 a modrá úsečka je škálována tak, že tato tečka je umístěna na konci červené úsečky délky 2. Při násobení libovolným X bude modrá tečka vždy začínat na pozici 1 a končit na pozici X. To funguje i pro X menší než 1 nebo záporné.
Opakem násobení je dělení.
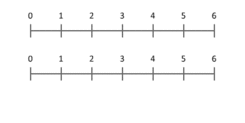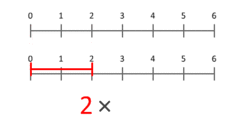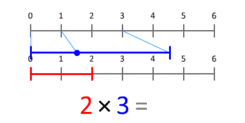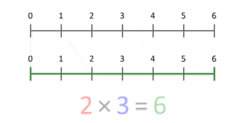
Tabulka násobení
Při výuce násobení učitelé obvykle vyžadují, aby si žáci zapamatovali tabulku prvních 9 čísel.
| Tabulka 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabulka násobení | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Související stránky
- Dodatek
- Číslo čtverce
- Odčítání
Otázky a odpovědi
Otázka: Co je to násobení?
Odpověď: Násobení je v matematice aritmetická operace pro zjištění součinu dvou čísel. Často se označuje symboly × a ⋅.
Otázka: Jak se nazývají dvě čísla, která se mají násobit?
Odpověď: Dvě čísla, která se mají násobit, se nazývají "koeficienty" nebo zvlášť "násobek" a "násobitel".
Otázka: Je násobení komutativní?
Odpověď: Ano, o násobení čísel se říká, že je komutativní - když pořadí čísel nemá vliv na hodnotu součinu. To platí pro celá čísla, racionální čísla, reálná čísla a komplexní čísla. Neplatí to však pro kvaterniony, vektory nebo matice.
Otázka: Jak můžeme interpretovat násobení kardinálních čísel?
Odpověď: Násobení kardinálních čísel můžeme interpretovat jako škálování veličin - když jedno číslo (multiplikant) škálujeme tak, že tečka umístěná na pozici 1 skončí v určitém bodě (multiplikátor).
Otázka: Jak znázorníte násobení tří číslem pět?
Odpověď: Trojku vynásobenou pěti můžeme zapsat jako 3 × 5 = 15 nebo vyslovit jako "tři krát pět se rovná patnáct".
Otázka: Co je opakem násobení?
Odpověď: Opakem násobení je dělení.
Vyhledávání