Algoritmus

Porovnání algoritmů

Problém lze obvykle vyřešit více než jedním způsobem. Může existovat mnoho různých receptů na přípravu určitého pokrmu, který vypadá jinak, ale nakonec chutná stejně, když je vše hotovo. Totéž platí pro algoritmy. Některé z těchto způsobů však budou lepší než jiné. Pokud recept vyžaduje spoustu složitých ingrediencí, které nemáte, není tak dobrý jako jednoduchý recept. Když se díváme na algoritmy jako na způsob řešení problémů, často chceme vědět, jak dlouho by počítači trvalo vyřešit problém pomocí určitého algoritmu. Když píšeme algoritmy, chceme, aby náš algoritmus zabral co nejméně času, abychom mohli náš problém vyřešit co nejrychleji.

Při vaření jsou některé recepty náročnější než jiné, protože jejich dokončení zabere více času nebo je třeba sledovat více věcí. Stejné je to i u algoritmů a algoritmy jsou lepší, když jsou pro počítač jednodušší. Věci, která měří obtížnost algoritmu, se říká složitost. Když se ptáme, jak je algoritmus složitý, často chceme vědět, jak dlouho bude počítači trvat vyřešit problém, který chceme, aby vyřešil.

Třídění

Toto je příklad algoritmu pro třídění barevných karet na hromádky stejné barvy:

1. Zvedněte všechny karty.
2. Vyberte si kartu z ruky a podívejte se na její barvu.
3. Pokud již existuje hromádka karet této barvy, položte tuto kartu na tuto hromádku.
4. Pokud nemáte žádnou hromádku karet této barvy, vytvořte novou hromádku pouze této barvy.
5. Pokud máte v ruce ještě nějakou kartu, vraťte se ke druhému kroku.
6. Pokud v ruce ještě nemáte žádnou kartu, karty se seřadí. Tím jste skončili.

Třídění podle čísel

Jedná se o příklady algoritmů pro třídění hromady karet s mnoha různými čísly tak, aby byla čísla seřazena.

Hráči začínají s hromádkou karet, které nebyly roztříděny.

První algoritmus

Tento algoritmus prochází hromádku karet po jedné kartě. Tato karta je porovnána s další kartou na hromádce. Všimněte si, že tato pozice se mění pouze v kroku 6. Tento algoritmus se nazývá bublinové třídění. Je pomalý.

1. Pokud je hromádka karet prázdná nebo obsahuje pouze jednu kartu, je roztříděna a vy jste skončili.
2. Vezměte si hromádku karet. Podívejte se na první kartu (horní) z hromádky.
3. Karta, na kterou se díváte, je karta A. Pozice, na které se karta A právě nachází, je v hromádce P.
4. Pokud za kartou A nejsou v hromádce žádné další karty, přejděte ke kroku 8.
5. Další kartou na hromádce je karta B.
6. Pokud má karta B nižší číslo než karta A, prohoďte pozice karet A a B. Pamatujte si, že jste to udělali. Při výměně karet neměňte pozici P.
7. Pokud je na hromádce za pozicí P další karta, podívejte se na ni; vraťte se ke kroku 3.
8. Pokud jste v posledním tahu nevyměnili pozici žádné z karet, máte hotovo; hromádka karet je seřazena.
9. V opačném případě se vraťte ke kroku 2.

Příklad krok za krokem

Vezměme hromádku karet s čísly "5 1 4 2 8" a seřaďme ji od nejmenšího čísla po největší pomocí tohoto algoritmu. V každém kroku algoritmus porovnává prvky zapsané tučně. Vrchol hromádky karet je na levé straně.

První průchod:
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 4 2 8 ) Zde algoritmus porovná první dva prvky a prohodí je.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Tyto prvky jsou již seřazeny, takže je algoritmus nepřehazuje.
Druhý průchod:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )(
1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Nyní je hromádka karet již seřazena, ale náš algoritmus to neví. Algoritmus potřebuje jeden celý průchod bez výměny, aby věděl, že je setříděný.
Třetí průchod:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Nakonec je pole seřazeno a algoritmus se může zastavit.

Historie

Jedná se o snadno pochopitelný algoritmus pro třídění. Počítačoví vědci ho nazvali Bubble sort, protože menší prvky se dostanou nahoru a v každém běhu se jejich pozice mění. Bohužel tento algoritmus není příliš dobrý, protože k seřazení potřebuje dlouhý čas (mnoho průchodů přes hromadu karet).

Druhý algoritmus

Tento algoritmus využívá jinou myšlenku. Někdy je řešení problému obtížné, ale problém lze změnit tak, aby se skládal z jednodušších problémů, které se řeší snadněji. Tomu se říká rekurze. Je sice obtížnější na pochopení než první příklad, ale poskytne lepší algoritmus.

Základní myšlenka

1. Pokud v hromádce nejsou žádné karty nebo je v ní pouze jedna karta, je hromádka roztříděna a vy jste skončili.
2. Rozdělte hromádku karet na dvě přibližně stejně velké poloviny. Pokud je počet karet lichý, bude mít jedna z obou hromádek o jednu kartu více než druhá.
3. Seřaďte každou z těchto dvou hromádek pomocí tohoto algoritmu (Pro každou hromádku začněte od položky 1 tohoto seznamu).
4. Sloučte obě seřazené hromádky dohromady, jak je popsáno níže.
5. Výsledkem je roztříděná hromádka karet. Jste hotovi.

Sloučení dvou zásobníků

To funguje se dvěma hromádkami karet. Jedna z nich se nazývá A, druhá B. Na začátku je prázdná třetí hromádka, která se nazývá C. Na konci bude obsahovat výsledek.

1. Pokud je hromádka A nebo B prázdná, položte všechny karty z hromádky, která není prázdná, na hromádku C; tím jste skončili, hromádka C je výsledkem sloučení. (Poznámka: vezměte celou hromádku a položte ji na hromádku C; když to budete dělat kartu po kartě, změní se pořadí a nebude to fungovat tak, jak by mělo.)
2. Podívejte se na horní karty hromádky A a hromádky B. Tu s nižším číslem položte na hromádku C. Pokud v hromádce C nebyly žádné karty, bude v ní nyní jedna karta.
3. Pokud v hromádce A nebo B zbývají karty, vraťte se ke kroku 1 a roztřiďte je.

Historie

Tento algoritmus vyvinul John von Neumann v roce 1945. Nenazýval ho Třídění podle čísel, ale Mergesort. Ve srovnání s jinými algoritmy je to velmi dobrý algoritmus pro třídění.

Třetí algoritmus

Prvnímu algoritmu trvá třídění karet mnohem déle než druhému, ale lze jej vylepšit (zdokonalit). Při pohledu na bublinové třídění si lze všimnout, že karty s vysokými čísly se z vrcholu hromádky přesouvají poměrně rychle, ale kartám s nízkými čísly na dně hromádky trvá dlouho, než se zvednou (přesunou na vrchol). Pro vylepšení prvního algoritmu je zde nápad:

Namísto porovnávání dvou karet, které jsou vedle sebe, se na začátku vybere "speciální" karta. Všechny ostatní karty se pak porovnávají s touto kartou.

1. Začínáme se zásobníkem A. Budou existovat další dva zásobníky B a C, které budou vytvořeny později.
2. Pokud hromádka A neobsahuje žádné karty nebo obsahuje pouze jednu kartu, jsme s tříděním hotovi.
3. Z hromádky A se vybere karta, pokud možno náhodně. Tomu se říká pivot.
4. Všechny zbývající karty hromádky A se porovnají s tímto pivotem. Karty s menším číslem jdou na hromádku B, karty se stejným nebo větším číslem jdou na hromádku C.
5. Pokud jsou nějaké karty v hromádkách B nebo C, je třeba tyto hromádky seřadit stejným algoritmem (začít na pozici 1 tohoto seznamu pro hromádku B i hromádku C).
6. Hotovo. Na seřazené hromádce karet je nejprve seřazená hromádka B, pak pivot a pak seřazená hromádka C.

Historie

Tento algoritmus vyvinul C. A. R. Hoare v roce 1960. Je to jeden z nejpoužívanějších algoritmů pro třídění v současnosti. Nazývá se Quicksort.

Animace, která ukazuje, jak funguje bublinové třídění


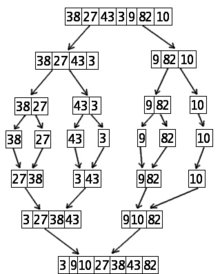
Třídění 7 čísel pomocí druhého algoritmu Třídění podle čísel (Mergesort)


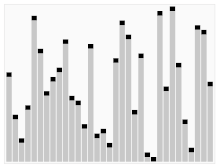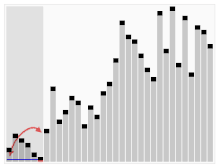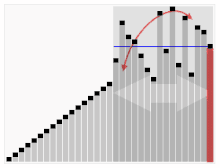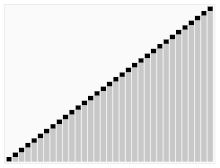
Třetí algoritmus pro třídění karet. Jako pivot je vybrán prvek s červeným pruhem. Na začátku je to prvek zcela vpravo. Tento algoritmus se nazývá Quicksort.

Sestavování algoritmů

Pokud mají hráči karty s barvami a čísly, mohou je seřadit podle barev a čísel, pokud provedou algoritmus "řazení podle barev", pak provedou algoritmus "řazení podle čísel" pro každou barevnou hromádku a pak je dají dohromady.

Algoritmy třídění podle čísel jsou obtížnější než algoritmy třídění podle barev, protože se může stát, že bude nutné opakovat jednotlivé kroky mnohokrát. Dalo by se říci, že třídění podle čísel je složitější.

Související stránky

• Euklidův algoritmus byl objeven před více než 2000 lety. Dokáže najít největšího společného dělitele dvou čísel.