Nerovnost (matematika)

Práce s nerovnostmi

Nerovnost v matematice je, když se dvě řešení nebo odpovědi porovnávají pomocí většího nebo menšího než. Je to tehdy, když se porovnávají dvě nebo ještě více řešení, která nejsou stejná. Řešit nerovnost znamená najít její řešení. Když dosadíte číslo do proměnné a tvrzení je pravdivé, pak se jedná o řešení. Když dosadíte číslo do proměnné a výrok není pravdivý, pak toto číslo není řešením výroku.

Nerovnost je nalezení řešení dané proměnné. Je to hledání relativního uspořádání množiny. Nerovnost má mnoho řešení, ale je třeba najít skutečné řešení. Nerovnost je řešení reálných čísel. Správný způsob čtení nerovnic je zleva doprava, stejně jako u ostatních rovnic, ale s tím rozdílem, že pro každou rovnici mají jiná pravidla.

Například x+4>12, kde x je reálné číslo. Nejprve je třeba najít x a zjistit, zda se jedná o řešení. Odpověď bude x>8 a to je pravdivé tvrzení. Tento výraz se týká umístění x v množině reálných čísel. Číselná přímka je jedním ze způsobů, jak znázornit umístění vzhledem ke všem ostatním reálným číslům (viz obrázek Nerovnost 1).

Nerovnost 1 Toto je řešení rovnice x+4>12

Různé druhy nerovností

Existuje pět různých druhů nerovností:

1. První z nich jsou lineární nerovnosti, což jsou nerovnosti, které rozlišují výrazy buď menší než nebo rovno, menší než nebo větší než nebo rovno, větší než. Je to taková, kterou když nahradíme nerovností za vztah rovná se, pak výsledkem bude lineární rovnice.
2. Druhou jsou kombinace nerovností, které mají splňovat nerovnosti, musíte mít v množinách řešení taková čísla, aby čísla splňující nerovnosti byla hodnotami v průsečíku obou množin řešení.
3. Třetí jsou nerovnosti zahrnující absolutní hodnoty, což znamená, že hodnoty lze přeformulovat jako kombinace nerovností, které budou zahrnovat absolutní hodnoty.
4. Čtvrtá z nich se nazývá polynomiální nerovnice, což znamená, že je spojitá, to znamená, že jejich grafy nemají žádné skoky ani zlomy.
5. V neposlední řadě je to racionální nerovnice, což znamená, že se jedná o tvar jednoho z mnohočlenů děleného mnohočlenem. Jinými slovy, grafy racionálních funkcí nemají žádné zlomy ani zastoupení u nul jmenovatele.

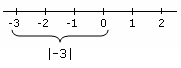
absolutní hodnota Příklad, který ukazuje absolutní hodnotu


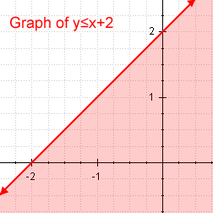
Lineární nerovnost Příklad lineární nerovnosti

Čtyři způsoby řešení nerovnic

Kvadratické rovnice lze řešit čtyřmi způsoby:

1. Pravidlo číslo jedna zní: na obou stranách musíte přičíst nebo odečíst stejné číslo.
2. Pravidlo číslo dvě spočívá v tom, že musíte posunout strany a změnit umístění znaménka nerovnosti.
3. Pravidlo číslo tři zní: Musíte násobit.
4. Pravidlo číslo čtyři zní, že stejné kladné nebo záporné číslo se dělí na obě strany. Ta však můžete použít pouze u snadných úloh o nerovnostech.

Kromě toho bude řešení nerovnosti vyžadovat dva kroky. Prvním z nich je zjednodušení pomocí reciprokého sčítání nebo odčítání. Druhým je další zjednodušení pomocí reciproké hodnoty násobení nebo dělení. Když násobíte nebo dělíte nerovnici záporným číslem, nezapomeňte symbol nerovnosti otočit.

příklad násobení nerovnosti


Příklad sčítání nerovností.

Příklady řešení nerovnic

Nerovnost je matematické tvrzení, které vysvětluje, že dvě hodnoty si nejsou rovny a liší se. Rovnice ab znamená, že a se nerovná b. Nerovnost je stejná s jakoukoli rovnicí, ale jediný rozdíl je v tom, že nerovnost nepoužívá znaménko rovnosti, místo toho používá symboly. Nerovnost b>a vyjadřuje, že b je větší než a. Rychlostní limity,značky a další používají k vyjádření nerovnosti.

Při řešení nerovnosti musí mít člověk pravdivý výrok. Když dělíte nebo násobíte nerovnici se záporným číslem na obou stranách, je výrok nepravdivý. aby byl výrok se záporným číslem správný, je třeba obrátit symbol, aby byl výrok správný. Když je číslo kladné, nemusíte symbol obracet. Nerovnost spočívá v tom, že výrok je pravdivý.

Začněte například pravdivým tvrzením -6y<-12. Když obě strany vydělíme číslem -6, výsledkem bude y< 2. V tomto výroku je třeba symbol obrátit, abychom měli pravdivý výrok, y>2 je správná odpověď. V číselné řadě (viz obrázek Nerovnost 2) upozorňuje uzavřený stínovaný kroužek na to, že je obsažen v množině řešení. Otevřený kruh upozorňuje na to, že není zahrnut v množině řešení.

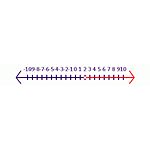
Nerovnost 2 Řešení rovnice -6y<-12

Související stránky

• Rovnost (matematika)
• Rovnice