Fraktál

Fraktál je jakýkoli obrazec, který při pohledu na obraz vytváří obraz, který při zvětšení vytvoří stále stejný obraz. Lze jej rozřezat na části, které vypadají jako zmenšená verze obrázku, s nímž se začínalo. Slovo fraktál vytvořil Benoît Mandelbrot v roce 1975 z latinského slova fractus, což znamená "rozbitý" nebo "roztříštěný". Jednoduchým příkladem je strom, který se větví na menší větve a ty na menší větve atd. Fraktály jsou nejen krásné, ale mají také mnoho praktických aplikací.

Sierpinskiho trojúhelník po 7 iteracích.

Mandelbrotova množina je známým příkladem fraktálu.

Příklady

Existuje mnoho typů fraktálů, které jsou tvořeny nejrůznějšími způsoby. Jedním z příkladů je Sierpinskiho trojúhelník, kde uvnitř velkého trojúhelníku je nekonečné množství malých trojúhelníků. Dalším příkladem je Mandelbrotova množina, pojmenovaná po Benoîtu Mandelbrotovi. Sierpinksiho trojúhelník je konstruován pomocí obrazců, ale Mandelbrotova množina je založena na rovnici.

V přírodě existuje také mnoho přírodních příkladů fraktálů, včetně stromů, sněhových vloček, některých druhů zeleniny a pobřeží.

Kochova křivka

Kochova křivka je jednoduchým příkladem fraktálu. Nejprve začněte s částí přímky - tzv. úsečkou. Úsečku rozřežte na 3 stejně velké části. Zbavte se středu těchto kousků a vložte do něj horní část trojúhelníku se stranami, které jsou stejně dlouhé jako kousek, který chcete vyříznout. Nyní máme 4 úsečky, které se na koncích dotýkají. To, co jsme právě provedli s první úsečkou, můžeme nyní provést s každým ze 4 kousků. Totéž nyní můžeme opakovat se všemi kousky, které nám nakonec zůstanou. Nyní to budeme dělat donekonečna a podíváme se, co nám nakonec vznikne.

Délka Kochovy křivky je nekonečná a plocha Kochovy křivky je nulová. To je docela zvláštní. Úsečka (s rozměrem 1) může mít délku 1, ale její plocha je 0. Čtverec o délce 1 a šířce 1 (s rozměrem 2) bude mít plochu 1 a délku nekonečno.

Rozměr podobnosti

Zdá se tedy, že Kochova křivka je větší než něco o rozměru 1 a menší než něco o rozměru 2. Smyslem dimenze podobnosti je poskytnout rozměr, který dává lepší představu o délce nebo ploše fraktálů. Pro Kochovu křivku tedy chceme dimenzi mezi 1 a 2.

Kochovu křivku lze rozřezat na čtyři části, z nichž každá má 1 3 {\displaystyle {\frac {1}{3}}} ${\frac {1}{3}}$ velikosti originálu. Počet částí, na které lze fraktál rozřezat, nazýváme N {\displaystyle N} $N$ , a rozdíl velikostí nazýváme B {\displaystyle B} $B$ . Tyto údaje dosadíme do rovnice:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}} ${\frac {\log N}{-\log B}}$

Kde log {\displaystyle \log } $\log$ je logaritmus čísla. Toto číslo je Hausdorffova dimenze fraktálu. V případě Kochovy křivky je to log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1,2619... } ${\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619...$ , jak jsme chtěli.

Kochova křivka je jedním z nejjednodušších fraktálních tvarů, a proto je snadné určit její rozměr. Její dimenze podobnosti i Hausdorffova dimenze jsou stejné. U složitějších fraktálů to neplatí.

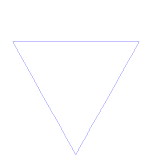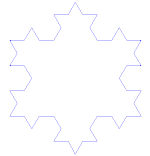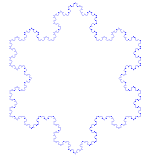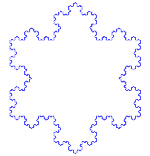
Kochova sněhová vločka

Kochova sněhová vločka (nebo Kochova hvězda) je stejná jako Kochova křivka, jen místo úsečky začíná rovnostranným trojúhelníkem.

Jak vytvořit Kochovu křivku

Používá

Fraktály mají mnoho aplikací, např. v biologii (plíce, ledviny, variabilita srdečního rytmu atd.), při zemětřeseních, ve financích, kde souvisí s tzv. těžkými chvostovými rozděleními, a ve fyzice. To naznačuje, že fraktály by se měly studovat, abychom pochopili, proč jsou fraktály v přírodě tak časté.

Některé fraktály existují pouze z uměleckých důvodů, jiné jsou však velmi užitečné. Fraktály jsou velmi efektivní tvary pro rádiové antény a používají se v počítačových čipech k efektivnímu propojení všech komponent. Také pobřežní linie lze považovat za fraktály.