Pí (číslo)

Aproximace

Pí se často píše formálně jako π nebo řecké písmeno π jako zkratka. Pí je také iracionální číslo, což znamená, že ho nelze zapsat jako zlomek ( a b {\displaystyle a \nad b} ), kde "a" a "b" jsou celá čísla (celá čísla). To v podstatě znamená, že číslice pí, které jsou napravo od desetinného čísla, se neopakují do nekonečna a že přesnou hodnotu pí nelze zapsat jako číslo. Pí lze pouze aproximovat nebo změřit na hodnotu, která je pro praktické účely dostatečně blízká.

Hodnota blízká pí je 3,141592653589793238462643... Běžná aproximace zlomku pí je 22 7 {\displaystyle 22 \over 7}. , což dává přibližně hodnotu 3,14285714. Tato aproximace je o 0,04 % vzdálena od skutečné hodnoty pí. Zatímco tato aproximace je akceptována pro většinu použití v reálném životě, zlomek 355 113 {\displaystyle 355 \over 113} je přesnější (dává přibližně 3,14159292) a může být použit, pokud je potřeba hodnota bližší pí. K získání lepší aproximace čísla pí lze použít počítače.

V březnu 2019 vypočítala Emma Haruka Iwao hodnotu pí na 31,4 bilionu číslic.

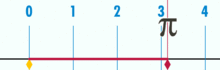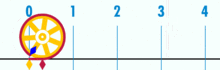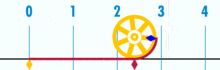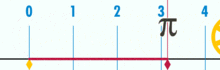
Diagram znázorňující, jak lze zjistit π pomocí kružnice o průměru jedna. Obvod této kružnice je π.

Historie

Hodnotu pí znali již staroindičtí matematici jako Bhaskaracharya a Aryabhatta.

Matematici znají číslo pí již tisíce let, protože stejnou dobu pracují s kružnicemi. Civilizace staré již od dob Babyloňanů dokázaly pí přiblížit mnoha číslicím, například zlomku 25/8 a 256/81. Většina historiků se domnívá, že staří Egypťané neměli o π žádnou představu a že tato shoda je náhodná.

První písemná zmínka o pí pochází z roku 1900 př. n. l. Kolem roku 1650 př. n. l. uvedl egyptský Ahmes hodnotu v papyru Rhind. Babyloňané dokázali zjistit, že hodnota pí je o něco větší než 3, a to tak, že jednoduše udělali velký kruh, na jeho obvod a průměr nalepili kousek provazu, zaznamenali jejich vzdálenosti a pak obvod vydělili průměrem.

Znalost čísla pí se dostala zpět do Evropy a do rukou Hebrejců, kteří toto číslo uvedli jako důležité v části Bible zvané Starý zákon. Poté bylo nejběžnějším způsobem, jak se pokusit zjistit číslo pí, nakreslit tvar o mnoha stranách uvnitř libovolného kruhu a pomocí plochy tohoto tvaru zjistit číslo pí. Například řecký filozof Archimédes použil k nalezení hodnoty pí tvar mnohoúhelníku, který měl 96 stran, ale Číňané v roce 500 n. l. dokázali k nalezení hodnoty pí použít mnohoúhelník o 16 384 stranách. Řekové, jako například Anaxagoras z Klazomenejí, se zabývali také zjišťováním dalších vlastností kruhu, například tím, jak z kružnic vytvořit čtverce a odmocnit číslo pí. Od té doby se mnoho lidí snažilo zjistit stále přesnější hodnoty čísla pí.

Historie pí
Filozof	Datum	Aproximace
Claudius Ptolemaios	kolem roku 150 n. l.	3.1416
Zu Chongzhi	430-501 N. L.	3.1415929203
al-Khwarizmi	kolem roku 800 n. l.	3.1416
al-Kashi	kolem roku 1430	3.14159265358979
Viète	1540-1603	3.141592654
Roomen	1561-1615	3.14159265358979323
Van Ceulen	kolem roku 1600	3.14159265358979323846264338327950288

V 16. století byly k dispozici stále lepší a lepší způsoby určení čísla pí, například složitý vzorec, který vyvinul francouzský právník François Viète. Řecký symbol "π" byl poprvé použit v eseji Williama Jonese z roku 1706.

Matematik jménem Lambert také v roce 1761 ukázal, že číslo pí je iracionální, tj. nelze ho zapsat jako zlomek podle běžných měřítek. Jiný matematik jménem Lindeman dokázal v roce 1882, že pí patří do skupiny čísel známých jako transcendentální čísla, což jsou čísla, která nemohou být řešením polynomické rovnice.

Pí lze kromě kružnic použít také k určení mnoha dalších věcí. Vlastnosti čísla pí umožnily jeho využití v mnoha dalších oblastech matematiky kromě geometrie, která se zabývá studiem tvarů. Mezi tyto oblasti patří komplexní analýza, trigonometrie a řady.

Pí v reálném životě

Dnes existují různé způsoby, jak vypočítat mnoho číslic čísla π. To má však omezený význam.

Pí lze někdy použít k určení plochy nebo obvodu libovolného kruhu. Chcete-li zjistit obvod kruhu, použijte vzorec C (obvod) = π krát průměr. Chcete-li zjistit plochu kruhu, použijte vzorec π (poloměr²). Tento vzorec se někdy zapisuje jako A = π r 2 {\displaystyle A=\pi r^{2}}. , kde r je proměnná pro poloměr libovolné kružnice a A je proměnná pro plochu této kružnice.

Výpočet obvodu kruhu s chybou 1 mm:

• Pro poloměr 30 metrů jsou potřeba 4 číslice.
• 10 číslic pro poloměr rovný poloměru Země
• 15 číslic pro poloměr rovný vzdálenosti Země od Slunce.

Lidé obvykle slaví 14. březen jako Den pí, protože 14. březen se také píše jako 3/14, což představuje první tři čísla 3,14 v aproximaci čísla pí. Den pí začal v roce 2001.

Související stránky

• Kruh