Kružnice

Kruh je kulatý dvourozměrný tvar. Všechny body na okraji kruhu jsou ve stejné vzdálenosti od středu.

Poloměr kruhu je přímka vedoucí ze středu kruhu do bodu na jeho straně. Matematici používají pro délku poloměru kruhu písmeno r. Střed kruhu je bod v samém středu.

Průměr kruhu (což znamená "po celé délce") je přímka, která prochází z jedné strany na druhou a přímo středem kruhu. Matematici pro délku této přímky používají písmeno d. Průměr kruhu se rovná dvojnásobku jeho poloměru (d se rovná 2 krát r).

d = 2 r {\displaystyle d=2\ r} $d=2\ r$

Obvod kruhu (což znamená "po celém obvodu") je přímka, která obíhá střed kruhu. Matematici pro délku této přímky používají písmeno C.

Číslo π (zapsané jako řecké písmeno pí) je velmi užitečné číslo. Je to délka obvodu dělená délkou průměru (π se rovná C děleno d). Jako zlomek se číslo π rovná přibližně ^22⁄7 nebo 335/113 (což je blíže) a jako číslo je to přibližně 3,1415926535.

Plocha a uvnitř kruhu se rovná poloměru vynásobenému sebou samým a pak vynásobenému π (a se rovná π krát r krát r).

Kruh

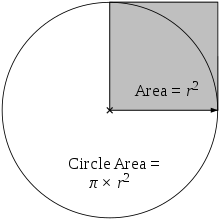
Plocha kruhu se rovná π násobku plochy šedého čtverce.

Výpočet π

π lze změřit nakreslením velkého kruhu a změřením jeho průměru (d) a obvodu (C). To proto, že obvod kruhu je vždy π násobkem jeho průměru.

π = C d {\displaystyle \pi ={\frac {C}{d}}} $\pi ={\frac {C}{d}}$

π lze také vypočítat pouze pomocí matematických metod. Většina metod používaných pro výpočet hodnoty π má žádoucí matematické vlastnosti. Jsou však těžko pochopitelné bez znalosti trigonometrie a počtů. Některé metody jsou však poměrně jednoduché, jako například tento tvar Gregoriho-Leibnizovy řady:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots } $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots$

Tuto řadu je sice snadné zapsat a vypočítat, ale není snadné pochopit, proč se rovná π. Snadněji pochopitelný přístup je nakreslit pomyslnou kružnici o poloměru r se středem v počátku. Pak každý bod (x,y), jehož vzdálenost d od počátku je menší než r, vypočtený podle pythagorovy věty, bude uvnitř kružnice:

d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Nalezení množiny bodů uvnitř kružnice umožňuje odhadnout plochu kružnice A. Například pomocí celočíselných souřadnic pro velké r. Protože plocha A kružnice je π krát poloměr na druhou, lze π aproximovat pomocí:

π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

Související stránky

Sféra

Otázky a odpovědi

Otázka: Co je to kruh?

Odpověď: Kruh je kulatý dvourozměrný útvar. Všechny body na okraji kružnice jsou ve stejné vzdálenosti od středu.

Otázka: Co matematici používají k vyjádření délky poloměru kruhu?

Odpověď: Matematici používají pro délku poloměru kruhu písmeno r.

Otázka: Co se v kružnicích zapisuje jako O?

Odpověď: Střed kružnice se často zapisuje jako O.

Otázka: Jak dlouhý je průměr kružnice?

Odpověď: Průměr (což znamená "po celé délce") kruhu je přímka, která vede z jedné strany na druhou a přímo středem kruhu. Je roven dvojnásobku jeho poloměru (d se rovná dvojnásobku r).

Otázka: Jaké písmeno používají matematici pro označení obvodu?

Odpověď: Matematici používají pro obvod písmeno C, což znamená "všude kolem".

Otázka: Jak můžeme vypočítat plochu uvnitř kruhu?

Odpověď: Plochu A uvnitř kruhu vypočítáme tak, že vynásobíme jeho poloměr sebou samým a pak vynásobíme ً (A se rovná ً krát r krát r).