Rychlost světla

Příklad

Toto chování se liší od našich běžných představ o pohybu, jak ukazuje tento příklad:

George stojí na zemi vedle kolejí (železnice). Kolem se řítí vlak rychlostí 48 km/h. George hodí baseballový míček rychlostí 140 km/h (90 mph) ve směru, kterým se pohybuje vlak. Tom, cestující ve vlaku, má zařízení (podobné radarové pistoli) na měření rychlosti hodu. Protože je ve vlaku, Tom se již pohybuje rychlostí 48 km/h (30 mph) ve směru hodu, takže Tom změří rychlost míčku pouze 97 km/h (60 mph).

Jinými slovy, rychlost baseballového míčku, kterou změří Tom ve vlaku, závisí na rychlosti vlaku.

Ve výše uvedeném příkladu se vlak pohyboval rychlostí 1/3 rychlosti míče a rychlost míče naměřená ve vlaku byla 2/3 rychlosti hodu naměřené na zemi.

Nyní zopakujte pokus se světlem místo baseballového míčku, tj. místo házení baseballovým míčkem má George baterku. George i Tom mají stejné zařízení na měření rychlosti světla (namísto radarové pistole v příkladu s baseballovým míčkem).

George stojí na zemi vedle vlakových kolejí. Kolem se řítí vlak rychlostí 1/3 rychlosti světla. George zabliká světelným paprskem ve směru, kterým se vlak pohybuje. George změří rychlost světla 186 282 mil za sekundu (299 792 km za sekundu). Tom, cestující ve vlaku, změří rychlost světelného paprsku. Jakou rychlost Tom změřil?

Intuitivně si můžeme myslet, že rychlost světla ze svítilny naměřená ve vlaku by měla být 2/3 rychlosti naměřené na zemi, stejně jako rychlost baseballového míčku byla 2/3. Ve skutečnosti je však rychlost naměřená ve vlaku plnou hodnotou, tedy 186 282 mil za sekundu (299 792 kilometrů za sekundu), nikoli 124 188 mil za sekundu (199 861 kilometrů za sekundu).

Zní to nemožně, ale právě to se měří. Důvodem je mimo jiné to, že světlo je energie, která se chová a pohybuje úplně jinak než hmota nebo pevné předměty, jako je baseballový míček.

Maxwellovy rovnice předpověděly rychlost světla a potvrdily myšlenku Michaela Faradaye, že světlo je elektromagnetické vlnění (způsob pohybu energie). Z těchto rovnic vyplývá, že rychlost světla souvisí s převrácenou druhou odmocninou permitivity volného prostoru, ε0, a permeability volného prostoru, μ0:

c = 1 ε 0 μ 0 . {\displaystyle c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ . }

Důsledkem této skutečnosti je, že nic nemůže letět rychleji než rychlostí světla. Dalším důsledkem je, že pro objekty, které mají hmotnost, platí, že bez ohledu na to, kolik energie se použije ke zvýšení rychlosti objektu, bude se objekt stále více přibližovat, ale nikdy nedosáhne rychlosti světla. Tyto myšlenky objevil na počátku 20. století Albert Einstein, jehož práce zcela změnila naše chápání světla.

Index lomu čirého materiálu je poměr mezi rychlostí světla ve vakuu a rychlostí světla v tomto materiálu.

Měření

Rømer

Ole Christensen Rømer použil astronomické měření k prvnímu kvantitativnímu odhadu rychlosti světla. Při měření ze Země jsou periody měsíců obíhajících kolem vzdálené planety kratší, když se Země k planetě přibližuje, než když se od ní vzdaluje. Vzdálenost, kterou světlo urazí od planety (nebo jejího měsíce) k Zemi, je kratší, když je Země v bodě své dráhy, který je nejblíže k planetě, než když je Země v nejvzdálenějším bodě své dráhy, přičemž rozdíl ve vzdálenosti odpovídá průměru oběžné dráhy Země kolem Slunce. Pozorovaná změna oběžné doby Měsíce je vlastně rozdíl v době, za kterou světlo překoná kratší nebo delší vzdálenost. Rømer tento efekt pozoroval u nejvnitřnějšího Jupiterova měsíce Io a odvodil, že světlu trvá 22 minut, než překoná průměr dráhy Země.

Bradley

Další metodou je využití aberace světla, kterou objevil a vysvětlil James Bradley v 18. století. Tento jev vzniká vektorovým součtem rychlosti světla přicházejícího ze vzdáleného zdroje (např. hvězdy) a rychlosti jeho pozorovatele (viz schéma vpravo). Pohybující se pozorovatel tak vidí světlo přicházející z trochu jiného směru a v důsledku toho vidí zdroj v poloze posunuté oproti jeho původní poloze. Vzhledem k tomu, že směr rychlosti Země se při jejím oběhu kolem Slunce neustále mění, způsobuje tento efekt pohyb zdánlivé polohy hvězd. Z úhlového rozdílu poloh hvězd lze vyjádřit rychlost světla v závislosti na rychlosti Země kolem Slunce. Tu lze při známé délce roku snadno převést na dobu potřebnou k cestě od Slunce k Zemi. V roce 1729 Bradley touto metodou odvodil, že světlo se pohybuje 10 210krát rychleji než Země po své dráze (moderní údaj je 10 066krát rychlejší), nebo ekvivalentně, že cesta světla od Slunce k Zemi trvá 8 minut a 12 sekund.

Moderní

Dnes se "světelný čas na jednotku vzdálenosti" - převrácená hodnota c (1/c), vyjádřená v sekundách na astronomickou jednotku - měří porovnáním doby, za kterou rádiové signály dosáhnou různých kosmických sond ve Sluneční soustavě. Poloha kosmických lodí se vypočítává z gravitačního působení Slunce a různých planet. Kombinací mnoha takových měření se získá nejvhodnější hodnota světelného času na jednotku vzdálenosti. K roku 2009^{[aktualizace] je} nejlepší odhad schválený Mezinárodní astronomickou unií (IAU) následující:

světelný čas na jednotku vzdálenosti: 499.004783836(10) s

c = 0,00200398880410(4) AU/s

c = 173,144632674(3) AU/den.

Relativní nejistota těchto měření je 0,02 částic na miliardu (2×10-11), což odpovídá nejistotě pozemských měření délky pomocí interferometrie. Vzhledem k tomu, že metr je definován jako délka, kterou světlo urazí za určitý časový interval, lze měření světelného času na jednotku vzdálenosti interpretovat také jako měření délky AU v metrech. Metr je považován za jednotku vlastní délky, zatímco AU se často používá jako jednotka pozorované délky v daném vztažném systému.

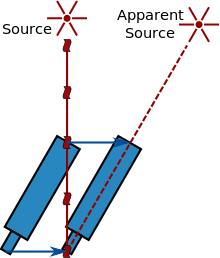
Aberace světla: světlo ze vzdáleného zdroje se v důsledku konečné rychlosti světla jeví pohybujícímu se dalekohledu jako světlo z jiného místa.

Praktické účinky

Konečná rychlost světla je hlavním omezením pro cestování vesmírem na velké vzdálenosti. Předpokládejme, že cesta na druhou stranu Mléčné dráhy by trvala přibližně 200 000 let. Ještě závažnější je, že žádná kosmická loď nemůže cestovat rychleji než světlo, takže veškerá doprava v galaktickém měřítku by byla fakticky jednosměrná a trvala by mnohem déle, než existuje jakákoli moderní civilizace.

Rychlost světla může být problematická i na velmi krátké vzdálenosti. V superpočítačích je rychlost světla limitem pro rychlost přenosu dat mezi procesory. Pokud procesor pracuje na frekvenci 1 gigahertz, může signál za jeden cyklus urazit maximálně 30 cm. Procesory proto musí být umístěny blízko u sebe, aby se minimalizovalo zpoždění komunikace; to může způsobit potíže s chlazením. Pokud se budou taktovací frekvence nadále zvyšovat, stane se rychlost světla nakonec limitujícím faktorem pro vnitřní konstrukci jednotlivých čipů.

Související stránky

• Michelson-Morleyho experiment