Harmonická řada

Historie

Skutečnost, že harmonická řada diverguje, poprvé dokázal ve 14. století Nicole Oresme, ale byla zapomenuta. Důkazy podali v 17. století Pietro Mengoli, Johann Bernoulli a Jacob Bernoulli.

Harmonické sekvence používají architekti. V období baroka je architekti používali v proporcích půdorysů, výškových úrovní a ve vztazích mezi architektonickými detaily kostelů a paláců.

Divergence

Existuje několik známých důkazů divergence harmonické řady. Několik z nich je uvedeno níže.

Srovnávací test

Jedním ze způsobů, jak dokázat divergenci, je porovnat harmonickou řadu s jinou divergentní řadou, kde je každý jmenovatel nahrazen nejbližší větší mocninou dvou:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+\cdots \end{aligned}}}

Každý člen harmonické řady je větší nebo roven příslušnému členu druhé řady, a proto součet harmonické řady musí být větší nebo roven součtu druhé řady. Součet druhé řady je však nekonečný:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}}

Z toho vyplývá (na základě srovnávacího testu), že i součet harmonických řad musí být nekonečný. Přesněji řečeno, výše uvedené srovnání dokazuje, že

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}})

pro každé celé kladné číslo k.

Tento důkaz, který navrhl Nicole Oresme kolem roku 1350, je považován za vrchol středověké matematiky. Dodnes se jedná o standardní důkaz, který se vyučuje v hodinách matematiky.

Integrální test

Je možné dokázat, že harmonická řada diverguje porovnáním jejího součtu s nevhodným integrálem. Uvažujme uspořádání obdélníků na obrázku vpravo. Každý obdélník je 1 jednotku široký a 1/n jednotek vysoký, takže celková plocha nekonečného počtu obdélníků je součtem harmonické řady:

plocha obdélníků = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{plocha}}\\{\text{obdélníky}}{konec{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Celková plocha pod křivkou y = 1/x od 1 do nekonečna je dána divergentním nevhodným integrálem:

plocha pod křivkou = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{oblast pod}}\\{\text{křivka}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty . }

Protože je tato plocha celá obsažena v obdélnících, musí být i celková plocha obdélníků nekonečná. To dokazuje, že

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1). }

Zobecnění tohoto argumentu je známé jako integrální test.

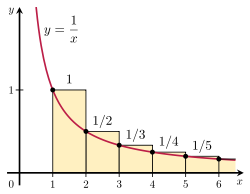
Ilustrace integrálního testu.

Míra divergence

Harmonická řada se rozchází velmi pomalu. Například součet prvních 1043 členů je menší než 100. Je to proto, že dílčí součty řady mají logaritmický růst. Konkrétně,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

kde γ je Eulerova-Mascheroniho konstanta a εk ~ 1/2k, která se s rostoucím k blíží k nule. Leonhard Euler dokázal jednak tuto skutečnost a také to, že součet, který zahrnuje pouze reciproké prvočísla, také diverguje, tj:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty . }

Dílčí součty

Prvních třicet harmonických čísel
n	Dílčí součet harmonické řady, Hn
	vyjádřeno jako zlomek		desetinné číslo	relativní velikost
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Konečné dílčí součty divergujících harmonických řad,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},}

se nazývají harmonická čísla.

Rozdíl mezi Hn a ln n konverguje k Eulerově-Mascheroniho konstantě. Rozdíl mezi libovolnými dvěma harmonickými čísly není nikdy celé číslo. Žádné harmonické číslo není celé, s výjimkou _H1 = 1.

Související řady

Střídavá harmonická řada

Série

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

je známá jako střídavá harmonická řada. Tato řada konverguje pomocí testu střídavé řady. Konkrétně se součet rovná přirozenému logaritmu 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}

Střídavá harmonická řada je sice podmíněně konvergentní, ale není absolutně konvergentní: pokud se členy řady systematicky přeskupí, součet se obecně změní a v závislosti na přeskupení může být i nekonečný.

Vzorec pro střídavou harmonickou řadu je speciálním případem Mercatorovy řady, Taylorovy řady pro přirozený logaritmus.

Související řadu lze odvodit z Taylorovy řady pro arktangens:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}. }

Tato řada je známá jako Leibnizova řada.

Obecné harmonické řady

Obecná harmonická řada má tvar

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

kde a ≠ 0 a b jsou reálná čísla a b/a není nula nebo záporné celé číslo.

Podle testu mezního srovnání s harmonickou řadou se všechny obecné harmonické řady rovněž rozcházejí.

řada p

Zobecněním harmonické řady je p-řada (nebo hyperharmonická řada), definovaná jako

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

pro libovolné reálné číslo p. Je-li p = 1, je řada p harmonickou řadou, která se rozchází. Buď integrální test, nebo Cauchyho kondenzační test ukazuje, že řada p konverguje pro všechna p > 1 (v takovém případě se nazývá nadharmonická řada) a diverguje pro všechna p ≤ 1. Je-li p > 1, pak součet p-řad je ζ(p), tj. funkce Riemannova zeta vyhodnocená v bodě p.

Problém nalezení součtu pro p = 2 se nazývá Basilejský problém; Leonhard Euler ukázal, že je to π2/6. Hodnota součtu pro p = 3 se nazývá Apéryho konstanta, protože Roger Apéry dokázal, že je to iracionální číslo.

Řada ln

S řadou p souvisí řada ln, která je definována jako

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

pro libovolné kladné reálné číslo p. To lze dokázat integrálním testem, který pro p ≤ 1 diverguje, ale pro všechna p > 1 konverguje.

Řada φ

Pro jakoukoli konvexní funkci reálné hodnoty φ, která je taková, že

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}}right)}{\varphi (u)}}<{\frac {1}{2}},}

série

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}\right)}

je konvergentní. ^[]

Náhodné harmonické řady

Náhodná harmonická řada

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

kde _sn jsou nezávislé, identicky rozdělené náhodné veličiny nabývající hodnot +1 a -1 se stejnou pravděpodobností 1/2, je v teorii pravděpodobnosti známým příkladem řady náhodných veličin, která konverguje s pravděpodobností 1. Skutečnost této konvergence je snadným důsledkem buď Kolmogorovovy věty o třech řadách, nebo úzce související Kolmogorovovy maximální nerovnosti. Byron Schmuland z University of Alberta dále zkoumal vlastnosti náhodné harmonické řady a ukázal, že konvergentní řada je náhodná veličina s některými zajímavými vlastnostmi. Zejména funkce hustoty pravděpodobnosti této náhodné veličiny vyhodnocená při +2 nebo při -2 nabývá hodnoty 0,124999999999999999999999999999764..., která se od 1/8 liší o méně než 10-42. Schmulandův článek vysvětluje, proč je tato pravděpodobnost tak blízko, ale ne přesně, 1/8. Přesná hodnota této pravděpodobnosti je dána nekonečným kosinovým součinem integrálu _C2 děleného π.

Vyčerpané harmonické řady

Lze ukázat, že ochuzená harmonická řada, v níž jsou odstraněny všechny členy, v nichž se kdekoli ve jmenovateli vyskytuje číslice 9, konverguje a její hodnota je menší než 80. Ve skutečnosti, když se odstraní všechny členy obsahující libovolný konkrétní řetězec číslic (v libovolném základu), řada konverguje.

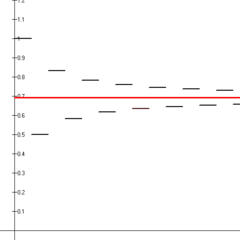
Prvních čtrnáct dílčích součtů střídavé harmonické řady (černé úsečky), které konvergují k přirozenému logaritmu 2 (červená čára).

Aplikace

Harmonická řada může být neintuitivní. Je to proto, že se jedná o divergentní řadu, přestože se její členy zmenšují a směřují k nule. Divergence harmonické řady je zdrojem některých paradoxů.

• "Červ na gumičce". Předpokládejme, že se po nekonečně pružné metrové gumičce plazí červ a zároveň je gumička rovnoměrně natažená. Jestliže se červ pohybuje 1 cm za minutu a gumička se natahuje 1 m za minutu, dosáhne červ někdy konce gumičky? Odpověď zní "ano", protože po n minutách je poměr vzdálenosti, kterou urazí červ, k celkové délce gumového pásu následující

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}. }

Protože s rostoucím n se řada libovolně zvětšuje, musí být nakonec tento poměr větší než 1, což znamená, že červ dosáhne konce gumičky. Hodnota n, při které k tomu dojde, však musí být extrémně velká: přibližně e100, což je číslo přesahující 1043 minut (1037 let). Harmonická řada se sice rozchází, ale velmi pomalu.

• Problém Jeepu se ptá, kolik celkového množství paliva potřebuje automobil s omezenou kapacitou pro přejezd pouště, přičemž na trase zůstávají kapky paliva. Vzdálenost, kterou může automobil ujet s daným množstvím paliva, souvisí s dílčími součty harmonických řad, které rostou logaritmicky. A tak množství potřebného paliva roste exponenciálně s požadovanou vzdáleností.

• Problém skládání kostek: je-li dána kolekce stejných kostek domina, je možné je poskládat na okraj stolu tak, aby visely přes okraj stolu, aniž by spadly. Protichůdným výsledkem je, že je lze poskládat tak, aby převis byl libovolně velký. Tedy za předpokladu, že je domina dostatek.

• Plavec, který při každém dotyku stěny bazénu zrychlí. Plavec začíná překonávat desetimetrový bazén rychlostí 2 m/s a s každým překonáním se k rychlosti přidávají další 2 m/s. Plavec je schopen překonat i desetimetrový bazén. Teoreticky je rychlost plavce neomezená, ale počet přeplavání bazénu potřebný k dosažení této rychlosti se stává velmi velkým; například k dosažení rychlosti světla (při zanedbání speciální teorie relativity) musí plavec přeplavat bazén 150 milionkrát. Na rozdíl od tohoto velkého čísla závisí čas potřebný k dosažení dané rychlosti na součtu řad při libovolném počtu překonání bazénu:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}. }

Výpočtem zjistíme, že doba potřebná k dosažení rychlosti světla je pouhých 97 sekund.

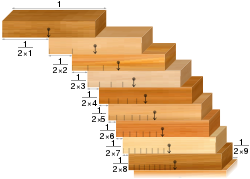
Problém skládání bloků: bloky uspořádané podle harmonické řady přemosťují štěpiny libovolné šířky.

Související stránky

• Harmonická progrese
• Seznam součtů reciprokých čísel