Hustota pravděpodobnosti
Funkce hustoty pravděpodobnosti je funkce, kterou lze definovat pro libovolné spojité rozdělení pravděpodobnosti. Integrál funkce hustoty pravděpodobnosti v intervalu [ a , b ] {\displaystyle [a,b]} ![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
dává pravděpodobnost, že daná náhodná veličina s danou hustotou je obsažena v daném intervalu.
Funkce hustoty pravděpodobnosti je nezbytná pro práci se spojitými rozděleními. Při hodu kostkou dostaneme čísla 1 až 6 s pravděpodobností 1 6 {\displaystyle {\tfrac {1}{6}}}. 
, ale to není spojitá funkce, protože jsou možná pouze čísla 1 až 6. Naproti tomu dva lidé nebudou mít stejnou výšku nebo stejnou hmotnost. Pomocí funkce hustoty pravděpodobnosti je možné určit pravděpodobnost pro lidi s výškou mezi 180 cm a 181 cm nebo mezi 80 kg a 81 kg, i když mezi těmito dvěma hranicemi je nekonečně mnoho hodnot.
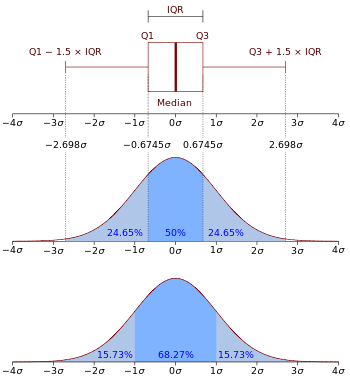
Boxplot a funkce hustoty pravděpodobnosti normálního rozdělení N(0, σ2) .
Otázky a odpovědi
Otázka: Co je to funkce hustoty pravděpodobnosti?
Odpověď: Funkce hustoty pravděpodobnosti je funkce, která charakterizuje jakékoliv spojité rozdělení pravděpodobnosti.
Otázka: Jak se zapisuje funkce hustoty pravděpodobnosti náhodné veličiny X?
Odpověď: Funkce hustoty pravděpodobnosti X se někdy zapisuje jako f_X(x).
Otázka: Co představuje integrál funkce hustoty pravděpodobnosti?
Odpověď: Integrál funkce hustoty pravděpodobnosti představuje pravděpodobnost, že daná náhodná veličina s danou hustotou je obsažena v daném intervalu.
Otázka: Je funkce hustoty pravděpodobnosti v celém svém oboru vždy nezáporná?
Odpověď: Ano, podle definice je funkce hustoty pravděpodobnosti nezáporná v celém svém oboru.
Otázka: Je součet integrace přes interval roven 1?
Odpověď: Ano, při integraci přes interval je součet roven 1.
Otázka: Jaký typ rozdělení charakterizuje funkce hustoty pravděpodobnosti?
Odpověď: Funkce hustoty pravděpodobnosti charakterizuje každé spojité rozdělení pravděpodobnosti.
