Pravděpodobnost
Pravděpodobnost je součástí aplikované matematiky. Zabývá se náhodou, studiem věcí, které se mohou stát, ale nemusí.
Pomocí pravděpodobnosti lze například ukázat, že když vyhodíte minci do vzduchu a necháte ji dopadnout, v polovině případů dopadne jednou stranou nahoru a v polovině případů druhou stranou nahoru. Mnoho mincí má na jedné straně obrázek tváře slavné osobnosti a na druhé straně něco jiného. Lidé často říkají straně s obličejem "hlava" a druhé straně "orel".
Pravděpodobnost události (p) je vždy mezi nulou (nemožné) a jedničkou (jisté).
Pokud hodíme kostkou (v množném čísle), pak je šance, že padne 1, 1/6 (to proto, že na kostce je 6 čísel). Šance, že padne 2, je také 1/6. To proto, že může padnout na 1, 2, 3, 4, 5 nebo 6. Šance, že padne libovolné číslo mezi 1 a 6, je 1. Pokaždé, když hodíme kostkou, padne vždy číslo mezi 1 a 6. To znamená, že kostka padne vždy na číslo mezi 1 a 6.
Pravděpodobnost lze zjistit pomocí matematiky. Pokud například hodíte šesti kostkami, pravděpodobnost, že vám padne číslo větší než deset, není zřejmá, ale lze ji zjistit pomocí matematiky a vědy.
Jednou z nejzajímavějších věcí na náhodě je, že pokud chcete zjistit pravděpodobnost, že se stanou dvě věci, vynásobte jejich dvě pravděpodobnosti dohromady. Předpokládejme například, že chcete zjistit pravděpodobnost, že hodíte dvěma kostkami a dostanete určitou kombinaci (mohou to být dvě šestky nebo trojka a pětka, prostě jakékoliv dvě). Možnost, že padne 3, je jedna ku šesti (⅙) a možnost, že padne 5, je také jedna ku šesti, takže pravděpodobnost, že padne 3 a pak 5, je ⅙×⅙=⅟36. Pokud toto číslo vyjádříme jako něco mezi 0 a 1, je to 0,027...7, což je poměrně málo. Možnost, že dostaneme 3, pak 5 a pak 2, by byla ⅙×⅙×⅙=⅟216 neboli 0,00463, což je mnohem nižší pravděpodobnost.
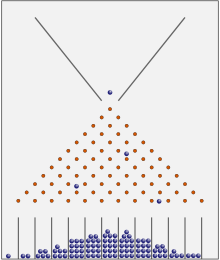
Ve stroji na fazole nebo v Galtonově krabici skončí většina kuliček blízko středu. Z dlouhodobého hlediska budou vykazovat normální rozdělení.
Představy o pravděpodobnosti
Lidé jako Jacob Bernoulli, Pierre-Simon Laplace nebo Christiaan Huygens používali slovo pravděpodobnost, jak je popsáno výše. Jiní lidé uvažovali o četnostech; tento pojem pravděpodobnosti se obvykle nazývá frekvenční pravděpodobnost.
Související stránky
- Seznam témat matematiky
- Teorie pravděpodobnosti
Otázky a odpovědi
Otázka: Co je to pravděpodobnost?
Odpověď: Pravděpodobnost je část aplikované matematiky, která se zabývá studiem věcí, které se mohou stát, ale nemusí.
Otázka: Jak lze pravděpodobnost vyjádřit?
Odpověď: Pravděpodobnost lze vyjádřit jako číslo mezi nulou (nemožné) a jedničkou (jisté).
Otázka: Jaký je příklad použití pravděpodobnosti?
Odpověď: Příkladem použití pravděpodobnosti je ukázat, že když vyhodíte minci do vzduchu a necháte ji dopadnout, v polovině případů dopadne jednou stranou nahoru a v polovině případů druhou stranou nahoru.
Otázka: Jak se vypočítá pravděpodobnost, že hodíte dvěma kostkami a získáte určitou kombinaci?
Odpověď: Pravděpodobnost, že hodíte dvěma kostkami a získáte určitou kombinaci, vypočtete tak, že vynásobíte jejich dvě pravděpodobnosti dohromady. Pokud byste například chtěli zjistit, zda padne 3 a pak 5, bylo by to 1/6 x 1/6 = 1/36.
Otázka: Co znamená slovo "tails", když mluvíme o mincích?
Odpověď: Když mluvíme o mincích, "ocas" označuje stranu, na které není obrázek.
Otázka: Jaká je pravděpodobnost, že při hodu šesti kostkami padne číslo větší než deset? Odpověď: Pravděpodobnost, že hodíte šesti kostkami a dostanete číslo větší než deset, lze zjistit pomocí matematiky a vědy, ale není zřejmá.
Otázka: Co se stane, když vynásobíte dvě pravděpodobnosti dohromady?
Odpověď: Když vynásobíte dvě pravděpodobnosti dohromady, počítáte pravděpodobnost, že se obě věci stanou najednou.
Vyhledávání