Planckova konstanta

Pozadí

Symboly použité v tomto článku.
Symbol Význam E Energie h Planckova konstanta k Boltzmannova konstanta c rychlost světla λ vlnová délka záření ν frekvence záření T absolutní teplota

Mezi lety 1670 a 1900 vědci diskutovali o podstatě světla. Někteří vědci se domnívali, že světlo se skládá z mnoha milionů malých částic. Jiní vědci se domnívali, že světlo je vlnění.

Světlo: vlny nebo částice?

V roce 1678 napsal Christiaan Huygens knihu Traité de la lumiere ("Pojednání o světle"). Domníval se, že světlo se skládá z vlnění. Tvrdil, že světlo se nemůže skládat z částic, protože světlo ze dvou paprsků se od sebe neodráží. V roce 1672 napsal Isaac Newton knihu Opticks. Domníval se, že světlo se skládá z červených, žlutých a modrých částic, které nazval korpuskulární. Newton to vysvětlil svým "pokusem se dvěma hranoly". První hranol rozkládal světlo na různé barvy. Druhý hranol sloučil tyto barvy zpět do bílého světla.

V 18. století byla největší pozornost věnována Newtonově teorii. V roce 1803 popsal Thomas Young "experiment s dvojitou štěrbinou". Při tomto experimentu světlo procházející dvěma úzkými štěrbinami interferuje samo se sebou. Vzniká tak obrazec, který ukazuje, že světlo se skládá z vln. Po zbytek devatenáctého století byla vlnové teorii světla věnována největší pozornost. V 60. letech 19. století James Clerk Maxwell vypracoval rovnice, které popisovaly elektromagnetické záření jako vlnění.

Teorie elektromagnetického záření považuje světlo, rádiové vlny, mikrovlny a mnoho dalších typů vln za totéž, jen mají různé vlnové délky. Vlnová délka světla, které vidíme očima, se pohybuje zhruba mezi 400 a 600 nm. Vlnová délka rádiových vln se pohybuje od 10 m do 1500 m a vlnová délka mikrovln je přibližně 2 cm. Ve vakuu se všechny elektromagnetické vlny šíří rychlostí světla. Frekvence elektromagnetického vlnění je dána vztahem:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}}.

Zde jsou definovány symboly.

Černé tělesové radiátory

Všechny teplé věci vyzařují tepelné záření, což je elektromagnetické záření. U většiny věcí na Zemi je toto záření v infračervené oblasti, ale něco velmi horkého (1000 °C nebo více) vydává viditelné záření, tedy světlo. Na konci 19. století mnoho vědců studovalo vlnové délky elektromagnetického záření ze zářičů černých těles při různých teplotách.

Zákon Rayleigh-Jeans

Lord Rayleigh poprvé zveřejnil základy Rayleighova-Jeansova zákona v roce 1900. Tato teorie byla založena na kinetické teorii plynů. Sir James Jeans publikoval úplnější teorii v roce 1905. Zákon se týká množství a vlnové délky elektromagnetické energie, kterou vydává zářič černého tělesa při různých teplotách. Rovnice, která jej popisuje, zní:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

Pro záření dlouhých vlnových délek výsledky předpovězené touto rovnicí dobře odpovídaly praktickým výsledkům získaným v laboratoři. Pro krátké vlnové délky (ultrafialové záření) však byl rozdíl mezi teorií a praxí tak velký, že si vysloužil přezdívku "ultrafialová katastrofa".

Planckův zákon

v roce 1895 Wien zveřejnil výsledky svých studií o záření černého tělesa. Jeho vzorec byl následující:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Tento vzorec fungoval dobře pro elektromagnetické záření krátkých vlnových délek, ale nefungoval dobře pro dlouhé vlnové délky.

V roce 1900 zveřejnil Max Planck výsledky svých studií. Pokusil se vytvořit výraz pro záření černého tělesa vyjádřený vlnovou délkou za předpokladu, že se záření skládá z malých kvant, a poté zjistit, co se stane, pokud se tato kvanta stanou nekonečně malými. (Jedná se o standardní matematický přístup). Výraz byl následující:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}.

Pokud necháme vlnovou délku světla velmi velkou, pak lze ukázat, že Raleigh-Jeansův a Planckův vztah jsou téměř totožné.

Vypočítal h a k a zjistil, že

h = 6,55×10 ⁻²⁷erg-sec.

k = 1,34×10 ⁻¹⁶erg-deg ^-1.

Tyto hodnoty se blíží současným uznávaným hodnotám 6,62606×10⁻³⁴ a 1,38065×10⁻¹⁶. Planckův zákon se dobře shoduje s experimentálními daty, ale jeho plný význam byl doceněn až o několik let později.

Kvantová teorie světla

Ukázalo se, že elektrony jsou fotoelektrickým jevem vytlačovány, pokud světlo dosáhne prahové frekvence. Pod touto hodnotou se z kovu nemohou uvolnit žádné elektrony. V roce 1905 Albert Einstein publikoval článek, ve kterém tento jev vysvětlil. Einstein navrhl, že světelný paprsek není vlna šířící se prostorem, ale spíše soubor diskrétních vlnových paketů (fotonů), z nichž každý má energii. Einstein uvedl, že tento jev je způsoben nárazem fotonu na elektron. Tím prokázal částicovou povahu světla.

Einstein také zjistil, že elektromagnetické záření s dlouhou vlnovou délkou nemá žádný účinek. Einstein tvrdil, že je to proto, že "částice" nemají dostatečnou energii, aby narušily elektrony.

Plank navrhl, že energie každého fotonu souvisí s frekvencí fotonu pomocí Planckovy konstanty. Matematicky by se to dalo zapsat takto:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}.

Plank obdržel Nobelovu cenu v roce 1918 za zásluhy o rozvoj fyziky, které prokázal svým objevem energetických kvant. V roce 1921 obdržel Einstein Nobelovu cenu za spojení Planckovy konstanty s fotoelektrickým jevem.

Ilustrace převzata z původního Newtonova dopisu Královské společnosti (1. ledna 1671 [juliánský kalendář]). S představuje sluneční světlo. Světlo mezi rovinami BC a DE je barevné. Tyto barvy se rekombinují a vytvářejí sluneční světlo na rovině GH


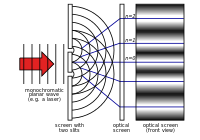
Youngův experiment s dvojitou štěrbinou


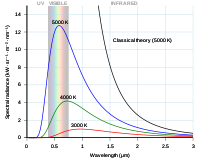
Rayleighova-Jeansova křivka a Planckova křivka v závislosti na vlnové délce fotonu.


Konference Solway 1911. Planck, Einstein a Jeans stojí. Planck je druhý zleva. Einstein je druhý zprava. Jeans je pátý zprava. Wien sedí, třetí zprava

Aplikace

Planckova konstanta má význam v mnoha aplikacích. Některé z nich jsou uvedeny níže.

Bohrův model atomu

V roce 1913 Niels Bohr zveřejnil Bohrův model struktury atomu. Bohr tvrdil, že úhlový moment elektronů obíhajících kolem jádra může nabývat jen určitých hodnot. Tyto hodnoty jsou dány rovnicí

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

kde

L = úhlový moment spojený s hladinou.

n = celé kladné číslo.

h = Planckova konstanta.

K výpočtu energie elektronů na jednotlivých hladinách lze použít Bohrův model atomu. Elektrony obvykle vyplňují nejnižší stavy atomu. Pokud atom obdrží energii například od elektrického proudu, elektrony budou excitovány do vyššího stavu. Poté elektrony klesnou zpět do nižšího stavu a ztratí svou dodatečnou energii tím, že vyzáří foton. Protože energetické hladiny mají určité hodnoty, budou mít fotony určité energetické hladiny. Takto vyzářené světlo lze pomocí hranolu rozdělit na různé barvy. Každý prvek má svůj vlastní vzor. Vzor pro neon je uveden vedle.

Heisenbergův princip neurčitosti

V roce 1927 zveřejnil Werner Heisenberg princip neurčitosti. Tento princip říká, že není možné provést měření, aniž by se měřená věc nenarušila. Stanovuje také hranici minimálního narušení způsobeného měřením.

V makroskopickém světě jsou tyto poruchy velmi malé. Pokud například měříme teplotu baňky s kapalinou, teploměr při zahřívání absorbuje malé množství energie. To způsobí malou chybu v konečném údaji, ale tato chyba je malá a není důležitá.

V kvantové mechanice je to jinak. Některá měření se provádějí na základě vzorce rozptýlených fotonů. Jedním z takových příkladů je Comptonův rozptyl. Pokud se měří poloha i hybnost částice, princip neurčitosti říká, že existuje kompromis mezi přesností, s níž se měří hybnost, a přesností, s níž se měří poloha. Rovnice, která popisuje tento kompromis, je následující:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

kde

Δp = nejistota hybnosti.

Δx = nejistota polohy.

h = Planckova konstanta.

Barva světelných diod

V elektrickém obvodu znázorněném vpravo závisí úbytek napětí na světelné diodě (LED) na materiálu LED. U křemíkových diod je tento úbytek 0,6 V. U LED diod se však pohybuje mezi 1,8 V a 2,7 V. Tato informace umožňuje uživateli vypočítat Planckovu konstantu.

Energie potřebná k přeskočení potenciálové bariéry jedním elektronem v materiálu LED je dána vztahem

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

kde

Q_e je náboj jednoho elektronu.

V_L je úbytek napětí na LED.

Když se elektron opět rozpadne, vyzáří jeden foton světla. Energie fotonu je dána stejnou rovnicí, jaká se používá u fotoelektrického jevu. Pokud tyto rovnice zkombinujeme, vlnová délka světla a napětí spolu souvisí takto

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}},}

Z tohoto vztahu lze vypočítat následující tabulku.

Barva	Vlnová délka (nm)	Napětí
červené světlo	650	1.89
zelené světlo	550	2.25
modré světlo	470	2.62

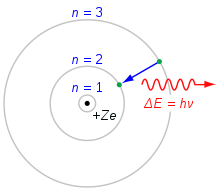
Bohrův model atomu. Elektron, který padá z obalu n=3 do obalu n=2, ztrácí energii. Tato energie se přenáší jako jeden foton.


Viditelné spektrum neonu. Každá čára představuje jiný pár energetických hladin.


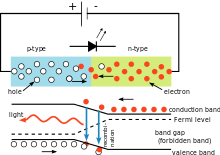
Jednoduchý obvod LED, který ilustruje použití Planckovy konstanty. Barva vyzařovaného světla závisí na úbytku napětí na diodě. Vlnovou délku světla lze vypočítat pomocí Planckovy konstanty.

Hodnota Planckovy konstanty a nová definice kilogramu

Od jeho objevu se měření h výrazně zlepšilo. Planck poprvé uvedl hodnotu h 6,55×10 ⁻²⁷erg-sec. Tato hodnota se pohybuje v rozmezí 5 % současné hodnoty.

Ke dni 3. března 2014 je nejlepší naměřená hodnota h v jednotkách SI 6,62606957×10⁻³⁴ J-s. Ekvivalentní hodnota v jednotkách cgs je 6,62606957×10 ⁻²⁷erg-sec. Relativní nejistota h je 4,4×10 ⁻⁸.

Redukovaná Planckova konstanta (ħ) je hodnota, která se někdy používá v kvantové mechanice. Je definována vztahem

ℏ = h 2 π {displaystyle \hbar ={\frac {h}{2\pi }}}.

V kvantové mechanice se někdy místo SI používají Planckovy jednotky. V této soustavě má redukovaná Planckova konstanta hodnotu 1, takže hodnota Planckovy konstanty je 2π.

Plancksovu konstantu lze nyní měřit s velmi vysokou přesností. To přimělo BIPM zvážit novou definici kilogramu. K definici kilogramu se již nepoužívá mezinárodní prototyp kilogramu. Místo toho BIPM definuje přesnou hodnotu Planckovy konstanty. Vědci používají tuto hodnotu a definice metru a sekundy k definici kilogramu.

 

Hodnota teoretické Planckovy konstanty

Planckovu konstantu lze také odvodit matematicky:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6,63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}{[0,9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6,63\krát 10^{-34}J\cdot s}

Zde μ 0 {\displaystyle \mu _{0}} je permeabilita volného prostoru, c {\displaystyle c} je rychlost světla, q 0 {\displaystyle q_{0}} je elektrický náboj elektronu, a 0 {\displaystyle a_{0}} je Bohrův poloměr a f 1 r {\displaystyle f_{1r}} je frekvence otáčení elektronu v atomu vodíku ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3,29\krát 10^{15}rev/s)} . Po dosazení těchto hodnot konstant do teoretické Planckovy konstanty se teoretická hodnota Planckovy konstanty přesně rovná experimentální hodnotě.

Související stránky

• Dualita vlny a částice