Princip neurčitosti

Diagramy

6. Tato animace ukazuje jeden z důležitých důsledků neurčitosti vesmíru: kvantové tunelování elektronů. Podívejte se pozorně. Pokaždé se přes bariéru dostane malý kousek.


5. Zavěšení středové mezery pomocí pružinových vah umožňuje měřit hybnost, ale mezera se přitom nepředvídatelně pohybuje, takže se ztrácí informace o poloze každého fotonu uprostřed.


4. Pružina upevněná na bariéře s malým otvorem způsobí, že se částice otvorem protlačí, čímž se bariéra zatlačí, pružiny se roztáhnou a změří se hybnost. Protože se však bariéra namontovaná na pružině pohybuje, máme menší jistotu, kde se částice nacházela, když prošla otvorem, a její polohu na detekční obrazovce ovlivní také difrakce.


3. Zúžením otvoru se zvýší jistota, kde se foton uprostřed nachází, ale jeho směr odtamtud k detekčnímu stínítku vpravo se pak stává odpovídajícím způsobem nejistějším. Zaostření se stává neostrým. Rozšířením otvoru se všechny fotony ocitnou ve středu detekční obrazovky, ale pak máme menší představu o tom, kde se nacházely, když procházely centrální bariérou.


1. Fotony, elektrony a další subatomární částice se při průletu velkým otvorem zaostří, ale nevíme přesně, kde se nacházely uprostřed dráhy.


2. Zúžení otvoru ohýbá dráhy částic kolem okrajů otvoru (difrakce), takže výsledný paprsek je větší a měkčí.

Jak se lidé dozvěděli o nejistotě?

Velmi krátce poté, co Werner Heisenberg vytvořil novou kvantovou fyziku, vyšlo z jeho matematiky něco neočekávaného - výraz:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Rozsah chyby polohy (x) krát rozsah chyby hybnosti (p) je přibližně stejný nebo větší než Planckova konstanta dělená 4π.

Tyto symboly vyjadřují v matematické podobě to, co jste již viděli na obrázcích výše. Symboly jasně říkají, že si nemůžete být zcela jisti, kde se něco nachází a kam to směřuje. Pokud si ujasníte, kde to v daném okamžiku je, pak máte menší představu o tom, kam to jde a jak rychle. Pokud si uděláte jasnější představu o tom, kam to jde a jak rychle, v kterémkoli okamžiku, pak máte menší představu o tom, kde to je právě teď.

Vědci již dříve zjistili, proč některé látky vydávají charakteristické barvy světla, když jsou zahřívány nebo jinak excitovány. Heisenberg se snažil vysvětlit, proč má každá z těchto barev charakteristický jas. Nestačilo by, kdyby on a ostatní vědci prostě řekli: "No, tak to prostě je." A tak se stalo. Byli si jisti, že pro tyto rozdíly a pro to, že poměry mezi intenzitami jasových čar jsou u každého vzorku prvku vždy stejné, musí existovat dobrý důvod.

Netušil, že narazí na skryté tajemství přírody, když se vydal objevit vysvětlení intenzity barevných čar charakteristických pro jednotlivé prvky. Studium kvantové mechaniky již dříve ukázalo, proč má vodík čtyři jasné čáry v té části spektra, kterou člověk vidí. Muselo se zdát, že další věcí, kterou je třeba se naučit, je jednoduše vypočítat jejich jas. Zdálo se, že vodík je zřejmým místem, kde začít, protože má pouze jeden elektron, s nímž se musí pracovat, a pouze čtyři čáry ve viditelné části spektra. Jistě musí existovat dobrý důvod, proč nejsou stejně jasné. Vysvětlení jasnosti různobarevných čar neonu a ostatních prvků mohlo počkat.

 

Heisenberg začal pracovat na kvantové fyzice úpravou klasických rovnic pro elektřinu, které jsou zpočátku velmi komplikované, takže matematika v jeho článku z roku 1925 byla velmi obtížná.

Snažil se najít správný způsob výpočtu intenzity jasných čar ve spektru vodíkové lampy. Musel najít související veličinu zvanou "amplituda" a vynásobit amplitudu amplitudou (jinými slovy musel amplitudu odmocnit), aby získal požadovanou intenzitu. Musel přijít na to, jak vyjádřit amplitudu způsobem, který by zohlednil skutečnost, že vodíkové lampy nevyzařují na všech frekvencích a nevyzařují v souvislém rozsahu frekvencí v té části spektra, kterou lidé vidí. Heisenberg našel nový pozoruhodný způsob výpočtu amplitudy.

Podivná rovnice|rovnice, kterou Heisenberg objevil a použil k násobení jedné kvantové veličiny (např. polohy) druhou (např. hybnosti), byla publikována v takzvaném "Heisenbergově 'magickém' článku z července 1925".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Výše uvedená matematika vypadá velmi obtížně, ale matematika, která k ní vede, je mnohem těžší a je velmi obtížné ji pochopit. Uvádíme ji zde jen proto, abychom ukázali, jak vypadala. Heisenbergův článek je historickým mezníkem. Mnoho fyziků, kteří jeho článek četli, prohlásilo, že nemohou nesouhlasit s jeho závěry, ale že nemohou pochopit jeho vysvětlení, jak k těmto závěrům dospěl. Počáteční rovnice, které Heisenberg použil, zahrnovaly Fourierovy řady a zahrnovaly mnoho faktorů. K výše uvedené rovnici se ještě vrátíme, protože je jakýmsi receptem na zápis a násobení matic.

Nové rovnice musely být tak zvláštní a neobvyklé, protože Heisenberg popisoval zvláštní svět, ve kterém se některé věci, jako například dráhy elektronů, pomalu nezvětšují ani nezmenšují. Nové druhy změn zahrnují skoky a velké mezery mezi skoky. Elektrony mohou přeskakovat pouze mezi určitými orbitami a energie získaná nebo ztracená při změně mezi orbitami vzniká při pohlcení fotonu o správné energii nebo při vzniku nového fotonu o správné energii. Pokud elektrony v atomech vodíku nejčastěji přeskakují (padají) mezi dvěma určitými orbitami, pak se na této energetické hladině vyzáří více fotonů, a proto bude světlo produkované na této hladině nejintenzivnější.

Bylo obtížné přizpůsobit rovnice sestavené pro spojitá spektra (to, co vidíte, když projde sluneční světlo hranolem) spektrům, která mají jen několik špičkových frekvencí, mezi nimiž není nic. Téměř všechno, co se dosud o světle a energii naučili, bylo provedeno s velkými objekty, jako jsou hořící svíčky nebo slunce, a všechny tyto velké objekty vytvářejí spojitá spektra. Přestože se s těmito věcmi běžné velikosti daly snadno provádět experimenty, trvalo ještě dlouho, než se přišlo na zákony (fyzikální), kterými se řídí. Nyní se fyzikové zabývali věcmi příliš malými, které nevytvářejí spojitá spektra, a snažili se najít způsob, jak z toho, co již znali, získat alespoň vodítka, která by jim pomohla najít zákony těchto malých a mezerovitých zdrojů světla.

Původní rovnice se zabývaly druhem vibrujícího tělesa, které by vytvářelo vlnění, podobně jako jazýček ve varhanách vytváří zvukovou vlnu o charakteristické frekvenci. Docházelo tedy k pohybu dopředu a dozadu (jako při vibraci rákosu) a k vyzařování vlny, kterou bylo možné zakreslit do grafu jako sinusoidu. Mnoho z toho, co se dříve zjistilo o fyzice na atomové úrovni, souviselo s elektrony pohybujícími se kolem jader. Když se hmota pohybuje po oběžné dráze, když se otáčí kolem nějakého náboje, má to, čemu se říká "úhlový moment". Úhlový moment je způsob, jakým se něco jako kolotoč bude otáčet i poté, co ho lidé přestanou tlačit. Matematika používaná pro výpočty fáze a úhlového momentu hybnosti je složitá. Navíc Heisenberg ve svém článku z roku 1925 neukázal všechny své výpočty, takže i dobří matematici mohou mít problém doplnit to, co neřekl.

Přestože mnozí fyzikové tvrdili, že nedokážou pochopit jednotlivé matematické kroky v Heisenbergově průlomovém článku, jeden nedávný článek, který se snaží vysvětlit, jak Heisenberg ke svému výsledku dospěl, má dvacet stránek plných matematiky. Ani tento článek není snadné pochopit. Matematika začínala opravdu těžkými věcmi a nakonec by dala něco relativně jednoduchého, co je uvedeno v horní části tohoto článku. Dostat se k jednoduššímu výsledku nebylo snadné a my se nebudeme snažit ukázat proces, jak se od zastaralého obrazu vesmíru dostat k nové kvantové fyzice. Potřebujeme jen dostatek podrobností, abychom ukázali, že téměř okamžitě poté, co Heisenberg učinil svůj průlom, se objevila část fungování vesmíru, kterou nikdo předtím neviděl.

Heisenberg musel být velmi nadšený, ale také velmi unavený, když pozdě v noci konečně učinil průlom a začal si dokazovat, že to bude fungovat. Téměř okamžitě si všiml něčeho zvláštního, něčeho, co považoval za otravný malý problém, který by mohl nějak odstranit. Ukázalo se však, že tato malá nepříjemnost je velkým objevem.

Heisenberg pracoval na násobení amplitud amplitudami a nyní měl Heisenberg dobrý způsob, jak vyjádřit amplitudu pomocí své nové rovnice. Přirozeně přemýšlel o násobení a o tom, jak by násobil věci, které jsou dány složitými rovnicemi.

Heisenberg si uvědomil, že kromě odmocňování amplitudy bude chtít nakonec násobit polohu hybností nebo násobit energii časem, a zdálo se, že bude mít význam, když v těchto nových případech pořadí otočí. Heisenberg se domníval, že by nemělo záležet na tom, zda se násobí poloha hybností, nebo zda se násobí hybnost polohou. Kdyby šlo jen o prostá čísla, nebyl by v tom žádný problém. Ale v obou případech šlo o složité rovnice a ukázalo se, že způsob, jakým se čísla do rovnic dosazují, se liší podle toho, jakým způsobem se začalo. V přírodě jste museli změřit polohu a pak změřit hybnost, nebo jste museli změřit hybnost a pak změřit polohu, a v matematice panovala stejná obecná situace. (Pokud se chcete dozvědět roztodivné podrobnosti, podívejte se na anglickou Wikipedii na článek Heisenberg's entryway to matrix mechanics!) Drobné, ale otravné rozdíly mezi výsledky měly zůstat, bez ohledu na to, jak moc si Heisenberg přál, aby zmizely.

Heisenberg se tehdy nemohl zbavit tohoto malého problému, ale byl vyčerpaný, a tak odevzdal svou práci svému přímému nadřízenému Maxi Bornovi a odjel na dovolenou.

Max Born byl pozoruhodný matematik, který brzy pochopil, že rovnice, kterou mu Heisenberg dal, je jakýmsi receptem na zápis matice. Doktor Born byl v té době jedním z mála lidí, kteří se zajímali o tento zvláštní druh matematiky, o němž si většina lidí myslela, že se k ničemu moc nehodí. Věděl, že matice lze násobit, takže provedení všech výpočtů pro započítání jednoho fyzikálního problému lze zvládnout vynásobením jedné matice druhou. Už jenom to, že dokázal složitý postup převést do standardní a přijatelné podoby, by mu usnadnilo práci. Mohlo by to také usnadnit jeho přijetí ostatními lidmi.

Born byl tak dobrý matematik, že si téměř okamžitě uvědomil, že změna pořadí násobení obou matic by vedla k jinému výsledku a výsledky by se lišily jen o málo. Tato hodnota by byla h/2πi. V běžném životě by tento rozdíl byl tak malý, že bychom ho ani nepostřehli.

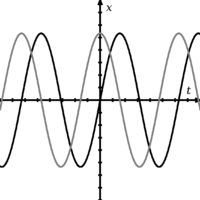
Dvě vlny, které nejsou ve vzájemné fázi.


Celé vizuální spektrum slunce. Nejsou zde žádné mezery. Tento graf ukazuje intenzity na různých frekvencích.


Neonové spektrum


Vodíkové spektrum


Když jsou určité molekuly excitovány, vyzařují charakteristickou barvu.

K formální teorii neurčitosti

Trvalo to několik let, ale Heisenbergovi se podařilo dokázat princip neurčitosti, který říká, že Δx × Δp = h/2, což je číslo, které vychází z původních rovnic, ale vynechává π a i, které souvisí s fázovými změnami. Heisenberg vysvětlil, že svůj princip neurčitosti odvodil z tohoto dřívějšího výsledku, když v roce 1927 napsal článek, v němž tuto teorii představil.

Konstanta psaná h, nazývaná Planckova konstanta, je záhadné číslo, které se často vyskytuje, a proto musíme pochopit, co je toto malé číslo zač. Číselně se obvykle udává jako 6,62607×10^-34 J s (joulových sekund). Jedná se tedy o veličinu, která zahrnuje energii a čas.

Byl objeven, když si Planck uvědomil, že energie dokonalého zářiče (tzv. zářiče černého tělesa) je vyzařována v jednotkách určité velikosti zvaných "kvanta" (v jednotném čísle je toto slovo "kvantum"). Vyzářená energie je vyzařována jako fotony a frekvence fotonu je úměrná "úderu", který dává. Různé frekvence viditelného světla vnímáme jako různé barvy. Na fialovém konci spektra má každý foton relativně velké množství energie; na červeném konci spektra má každý foton relativně malé množství energie. Způsob výpočtu množství energie fotonu je dán rovnicí E = hν (energie se rovná Planckově konstantě krát "nu" neboli frekvence).

Heisenbergův princip neurčitosti Δx × Δp ≥ h nám říká, že kdykoli se snažíme určit určité dvojice čísel, můžeme se k nim jen přiblížit, a že pokud se pokusíme o zpřesnění jednoho z nich, tj. pokud se pokusíme zmenšit Δx, abychom měli lepší představu o poloze něčeho, budeme muset dostat zpět větší číslo pro druhé číslo z dvojice, a že velikost odchylky obou čísel úzce souvisí s h.

Další dvojice fyzikálních veličin se řídí vztahem neurčitosti: ΔE × Δt ≥ h, a tato dvojice mimo jiné naznačuje, že pokud se podíváme do mezihvězdného prostoru, tedy na nějaké místo, kde bychom vůbec nic nečekali, a budeme Δt snižovat stále blíže k nule, pak se pro udržení rovnováhy uvedené v rovnici musí ΔE stále zvětšovat - a najednou se může objevit něco, co má hybnost právě na tento krátký časový úsek.

Jak lze tuto neurčitost (nedostatek jistoty) vysvětlit? Co se děje ve vesmíru? Často se říká, že nová teorie, která je úspěšná, může poskytnout nové informace o zkoumaných jevech. Heisenberg vytvořil matematický model, který předpověděl správné intenzity pro spektrum jasných čar vodíku, ale aniž by to měl v úmyslu, zjistil, že určité dvojice fyzikálních veličin odhalují neočekávanou neurčitost. Do té doby nikdo netušil, že měření nelze donekonečna zpřesňovat a zpřesňovat. Skutečnost, že je nelze učinit jistějšími, přesnějšími, byla ohromujícím novým objevem. Mnozí lidé se s ním nechtěli smířit.

Bohr a jeho kolegové tvrdili, že fotony, elektrony atd. nemají ani polohu, ani hybnost, dokud nejsou změřeny. Tento teoretický postoj vyrostl z objevu neurčitosti a nebyl jen nějakou osobní preferencí, čemu věřit. Bohr tvrdil, že o něčem, jako je foton nebo elektron, nevíme nic, dokud to nepozorujeme. Abychom mohli takovou malou věc pozorovat, musíme s ní nějak interagovat. V běžném životě je možné dělat něco takového, jako chodit podél automobilu a přitom si zaznamenávat časy, kdy přejede body na mřížce nakreslené na chodníku. Možná, že hmotnost samotného automobilu bude stlačovat malé páčky v chodníku, které vypnou hodiny připevněné ke každé z nich a zaznamenají hmotnost automobilu. Nakonec bychom měli jasný záznam o tom, kde se automobil v různých časech nacházel, a také bychom mohli vypočítat směr jeho postupu a hmotnost. V každém okamžiku na hodinách bychom pak mohli znát jak jeho polohu, tak jeho hybnost (rychlost vynásobenou hmotností). Ani by nás nenapadlo, že síla potřebná k pohybu malých páček bude mít na postup auta nějaký vliv. Stejně tak bychom si nepředstavovali, že automobil nemá žádnou polohu ani trajektorii mezi body na chodníku, kde jsou páčky, nebo že automobil v těchto okamžicích existuje v jakési trojrozměrné šmouze a ustálí se pouze při stlačení páčky. Svět, který známe, tyto zvláštní druhy interakcí neodhaluje.

K určení polohy lodi na moři během nejtemnější noci bychom mohli použít reflektor, který by nenarušil polohu ani směr pohybu lodi, ale k určení polohy elektronu pomocí světla by bylo nutné zasáhnout jej jedním nebo více fotony, z nichž každý by měl dostatečnou hybnost, aby narušil polohu a trajektorii elektronu. Lokalizace elektronu jinými prostředky by vyžadovala jeho fyzické zadržení, které by rovněž ukončilo jeho pohyb vpřed.

Aby bylo možné foton lokalizovat, je nejlepší, co lze udělat, aniž by byl ukončen jeho dopředný pohyb, nechat ho projít kruhovým otvorem v bariéře. Známe-li čas, kdy byl foton vyslán (například laserem), a čas, kdy foton dorazí na detekční obrazovku, například digitální kameru, pak je možné vypočítat čas potřebný k uražení této vzdálenosti a čas, kdy foton procházel otvorem. Aby jím však foton mohl projít, musí mít kruhový otvor průměr větší, než je velikost fotonu. Čím menší je kruhová díra, tím blíže se přiblížíme k poznání přesné polohy fotonu při jeho průchodu. Nikdy však nemůžeme vědět, zda je foton v daném okamžiku mimo střed. Pokud je otvor přesně stejně velký jako foton, neprojde jím. Se zmenšujícím se průměrem díry se stále výrazněji mění hybnost neboli směr fotonu, který díru opouští.

Niels Bohr a jeho kolegové tvrdili, že se dostáváme do velkých potíží, pokud o věcech, které jsou příliš malé na to, abychom je viděli i mikroskopem, považujeme za pravdivé cokoli, pro co máme důkaz pouze v měřítku každodenního života. V každodenním životě mají věci vždy určitou polohu. V atomovém měřítku nemáme pro tento závěr žádný důkaz. V každodenním životě mají věci určitý čas, ve kterém se vyskytují. V atomovém měřítku nemáme pro tento závěr žádné důkazy. Pokud v běžném životě pozorujeme továrnu od noční směny prvního dne do denní směny druhého dne a vidíme hotový automobil, který se odváží do expedičního doku, nemělo by smysl tvrdit, že nelze říci, zda byl dodán během noční nebo denní směny. Na atomárním měřítku však můžeme ukázat případy, kdy musíme počítat jeden foton jako vyrobený ve dvou časech. (Pokud to nestačí, můžeme také ukázat případy, kdy je jeden foton vyprodukován dvěma sousedními lasery.)

Část potíží se zjišťováním toho, co se děje v atomárním měřítku, spočívá v tom, že bychom rádi věděli, kde se něco nachází a jaká je jeho trajektorie, a obě věci bychom chtěli znát ve stejném čase, ale nemůžeme měřit současně polohu i trajektorii. Buď změříme hybnost fotonu nebo elektronu v jednom okamžiku a pak bez většího zpoždění, než je nutné, změříme jeho polohu, nebo si to prohodíme a nejdříve změříme polohu a pak hybnost. Problém spočívá v tom, že tím, že první měření nabude docela určité podoby (tím, že ho nějakým způsobem stlačíme), zvýšíme nejistotu spojenou s dalším měřením. Pokud by naše počáteční měření byla tak hrubá, že by se do každého z nich vnášelo hodně chyb, pak bychom mohli věci zlepšit tím, že bychom při každém z nich použili lehčí dotyk, ale nikdy bychom se nedostali za určitou hranici přesnosti.

Z každodenního života víme, že pokus o vážení na koupelnové váze umístěné na pračce v odstřeďovacím cyklu vede k nepřesným výsledkům, protože jehla na váze se silně chvěje. Pračku můžeme vypnout. Pro velmi přesná měření však zjistíme, že jehla se třese i při průjezdu nákladních aut v okolí, takže můžeme váhu na něco položit, abychom ji izolovali od rušivých vlivů zvenčí. Věříme, že se nám podaří eliminovat vibrace natolik, že nám poskytnou výsledky právě tak přesné, jak chceme. Nikdy neuvažujeme o tom, že věc na váze sama vibruje nebo že má neurčitou hybnost.

Pokud budeme argumentovat zpětně na základě principu neurčitosti, zdá se, že ve skutečnosti neexistuje žádná definitivní poloha ani žádná definitivní hybnost pro žádnou věc v atomárním měřítku a že experimentátoři mohou věci donutit k definitivnosti pouze v mezích stanovených principem neurčitosti. Bohr a jeho kolegové pouze tvrdili, že bez měření nemůžeme nic vědět, a když měření provedeme, můžeme věci tlačit směrem k určitější poloze nebo určitější hybnosti, ale nemůžeme získat absolutní určitost nebo jistotu, kterou bychom chtěli. Jiní však tuto možnost brali vážně a tvrdili, že pokud je matematika správná, pak ve světě ultra malého nemůže existovat definitivnost nebo jistota. Podstatou vědy je, že matematika je pouze modelem reality a neexistuje žádná záruka, že je to model správný.

Matematika a praktické důsledky věcí, které matematika předpovídá, jsou natolik spolehlivé, že je velmi těžké s nimi nesouhlasit, ale to, co matematika říká o skutečném světě, přineslo několik různých myšlenek. Mezi vědci, kteří pracovali s Nielsem Bohrem v Kodani, byl princip neurčitosti chápán tak, že na elementární úrovni fyzikální vesmír neexistuje v deterministické podobě. Je spíše souborem pravděpodobností nebo potenciálů.

V rozporu s příběhem, který kolem matematiky utkala kodaňská skupina, existují i jiné příběhy, například "interpretace více vesmírů", která říká, že pokaždé, když existuje více možných výsledků podle kvantové teorie, každý výsledek se vyskytuje ve vlastním novém vesmíru. Einstein tvrdil, že více možných výsledků neexistuje, takže vesmír je jen jeden a je determinovaný, nebo, jak říkal, "Bůh nehraje v kostky".

Pokud by h bylo nejmenší možné množství energie, pak by základní rovnice udávající energii obsaženou ve fotonech různých frekvencí nebyla v rovnováze. Byla by špatná.

Námitky proti principu neurčitosti

Albert Einstein viděl, že nová kvantová mechanika předpokládá nedostatek polohy a hybnosti v době před měřením, a důrazně proti tomu protestoval. Byl pevně přesvědčen, že věci měly před měřením určitou polohu a určitý moment hybnosti a že skutečnost, že měření jedné z dvojice věcí a narušení možnosti přesně změřit druhou, nesvědčí o tom, že by předtím některá z nich chyběla. Spolu se svými dvěma kolegy napsal práci, která vešla ve známost jako "EPR článek". Tento článek tvrdí, že musí existovat charakteristiky, které určují polohu a hybnost, a že pokud bychom je mohli vidět nebo pokud bychom o nich mohli získat informace, pak bychom mohli polohu a hybnost matematicky poznat a předpovědět. Dlouhou dobu si lidé mysleli, že neexistuje způsob, jak dokázat nebo vyvrátit to, co bylo pro Einsteina článkem víry. Tento spor byl velmi produktivní, protože vedl k veškerému modernímu vývoji v oblasti entanglementu.

Z matematického hlediska se Einstein mýlil. V roce 1964 John Stewart Bell vyvinul matematickou metodu, která rozlišuje mezi chováním dvou částic, které mají determinované stavy, jež jsou pouze neznámé pro dva jedince, kteří je zkoumají, a dvou částic, které mají propletené stavy, které jsou neurčité nebo nejisté, dokud nejsou změřeny. Jeho metoda ukazuje, že pravděpodobnosti získání určitých výsledků se za těchto dvou různých předpokladů liší. Jeho práce se nazývá Bellova věta nebo Bellova nerovnost. Experimenty ukázaly, že příroda se chová tak, jak ji Bell popsal.

Další cesta k nejistotě

Původní diskuse o Heisenbergově principu neurčitosti vycházely z modelu, který neuvažoval, že částice hmoty, jako jsou elektrony, protony atd., mají vlnovou délku. V roce 1926 Louis de Broglie ukázal, že všechny věci, nejen fotony, mají svou vlastní frekvenci. Věci mají vlnovou i částicovou povahu, stejně jako fotony. Kdybychom se snažili vlnu věci, jako je proton, zúžit a zvýšit, byla by její poloha jasnější, ale pak by se hybnost hůře definovala. Pokud bychom se snažili zpřehlednit část popisu hybnosti vlny, tj. aby zůstala v užším rozmezí hodnot, pak by se vrchol vlny rozšířil a její poloha by se stala méně určitou.

Vlna, která je součástí popisu fotonu, není v kvantové mechanice stejným druhem vlny jako vlna na hladině oceánu nebo oblasti stlačeného a zředěného vzduchu, které tvoří zvukové vlny. Místo toho mají tyto vlny vrcholy nebo oblasti s vysokou amplitudou, které mají co do činění s pravděpodobností, že se v daném bodě v prostoru a čase něco nachází. Přesněji řečeno, je to čtverec amplitudy, který udává pravděpodobnost, že se nějaký jev objeví.

Vlna, která se vztahuje na foton, může být čistá sinusovka. V takovém případě by čtverec hodnoty každého vrcholu udával pravděpodobnost pozorování fotonu v daném bodě. Protože amplitudy sinusových vln jsou všude stejné, pravděpodobnost nalezení fotonu v každém z nich by byla stejná. Prakticky vzato by tedy znalost vlny pro jeden z těchto fotonů neposkytla vodítko, kde jej hledat. Na druhou stranu hybnost fotonu matematicky souvisí s amplitudou jeho vlny. Protože v tomto případě máme čistou sinusovku, je amplituda každého cyklu vlny stejná, a proto je s touto vlnou spojena pouze jedna hodnota hybnosti. Nevěděli bychom, kam foton dopadne, ale věděli bychom přesně, jak silně dopadne.

Ve světelných paprscích, které se soustředí na určitý bod na detekční obrazovce, nejsou vlny spojené s fotony čistě sinusové. Místo toho se jedná o vlny s vysokou amplitudou v jednom bodě a mnohem nižšími amplitudami po obou stranách tohoto nejvyššího vrcholu. Matematicky je možné takovou vlnu analyzovat na řadu různých sinusových vln o různých vlnových délkách. O něco jednodušší je představit si obrácený postup, když se podíváme na počáteční sinusovku o jedné frekvenci, ke které se přidá druhá sinusovka o jiné vlnové délce, pak třetí, pak čtvrtá atd. Výsledkem bude složená vlna vykazující jeden vysoký vrchol a obsahující velké množství vln různých vlnových délek, a tedy i různých momentů. V takovém případě je pravděpodobnost, že se foton objeví v určitém bodě, extrémně vysoká, ale může se ukázat, že hybnost, kterou přenáší, souvisí s vlnovou délkou některé ze složkových vln. Jinými slovy, hodnota p = ħ/λ již není jedinou hodnotou, protože je třeba vzít v úvahu všechny délky sestavených "vln různé vlnové délky".

Simulace ukazuje, jak matematicky modelovat zostření polohy částice: Na původní sinusovou vlnu je možné superponovat mnoho různých tvarů vln. Střed bude tvořit stále vyšší a vyšší vrchol a počet ostatních vrcholů se bude zvyšovat, ale jejich výška se bude snižovat, protože se budou navzájem rušit. Nakonec tedy v superpozici vznikne mnoho různých vln, každá s jinou vlnovou délkou a (podle p = ħ/λ) s jinou hybností, ale pouze jeden velmi vysoký vrchol, který roste a zužuje se a dává nám něco, co se stále více blíží k určité poloze.

Aby byl moment hybnosti stále určitější, museli bychom odebírat další a další překrývající se sinusovky, až by nám zbyla jen jednoduchá sinusovka. Přitom bychom postupně zmenšovali výšku centrálního vrcholu a postupně zvětšovali výšky konkurenčních míst, kde by se částice mohla nacházet.

Když tedy začneme s vlnovým obrazem subatomárních částic, budeme mít obvykle vždy co do činění s případy s relativně vysokými centrálními vrcholy a relativně mnoha vlnovými délkami složek. Za těchto okolností nikdy nebude možné předpovědět přesnou polohu nebo přesnou hybnost. Pokud je matematický model přesnou reprezentací skutečného světa, pak žádný foton ani jiná subatomární částice nemá ani přesnou polohu, ani určitou hybnost. Když takovou částici měříme, můžeme zvolit metodu, která pík ještě více stlačí a zúží, nebo můžeme zvolit metodu, která pík sníží a vyrovná vlnové délky jednotlivých složek. V závislosti na tom, co a jak měříme, můžeme dosáhnout toho, že naše poloha vyjde určitější, nebo můžeme zúžit rozsah hybnosti. Při navrhování experimentu můžeme dbát na to, abychom se vyhnuli různým způsobům, jak s aparaturou zahýbat, ale nemůžeme se zbavit toho, že na začátku nebylo nic zcela definitivní.

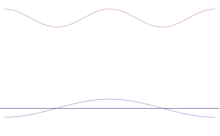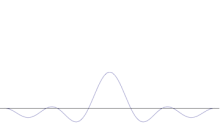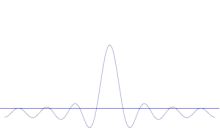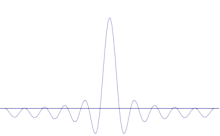
Superpozice několika rovinných vln. Vlnový paket se sčítáním mnoha vln stále více lokalizuje. Fourierova transformace je matematická operace, která rozdělí vlnový paket na jednotlivé rovinné vlny. Všimněte si, že zde zobrazené vlny jsou pouze pro ilustraci reálné, zatímco v kvantové mechanice je vlnová funkce obecně komplexní.

Kulturní vlivy

Největší vliv měl Heisenbergův princip neurčitosti na argumenty o svobodě vůle. V rámci teorií klasické fyziky je možné tvrdit, že zákony příčiny a následku jsou neúprosné a že jakmile vesmír začal určitým způsobem, lze z tohoto počátečního stavu vypočítat interakce veškeré hmoty a energie, které se v budoucnu vyskytnou. Protože vše je absolutně výsledkem toho, co tomu předcházelo, tvrdili, že každé rozhodnutí, které člověk učiní, a každá situace, do níž se dostane, byla od počátku času předem určena. Nemáme tedy žádnou možnost volby v tom, co děláme.

Lidé, kteří věří ve svobodu vůle, tvrdí, že zákony kvantové mechaniky nepředpovídají, co se stane, ale pouze to, co je více a co méně pravděpodobné. Proto je každý čin výsledkem série náhodných "hodů mincí" a žádné rozhodnutí nelze vysledovat zpět k souboru nutných předpokladů.

Výrazy "kvantový skok" a "kvantový skok" se staly běžnými způsoby, jak o věcech mluvit. Obvykle mají lidé v úmyslu popsat něco, co zahrnuje obrovskou změnu, ke které dojde v krátkém časovém období. Ve skutečnosti se tento výraz vztahuje na chování elektronu v atomu, když absorbuje foton přicházející zvenčí a přeskočí tak z jedné oběžné dráhy kolem jádra atomu na vyšší, nebo když vyzáří foton a spadne tak z vyšší oběžné dráhy na nižší. Myšlenka Neilse Bohra a jeho kolegů byla, že elektron se nepohybuje mezi orbitami, ale místo toho zmizí z jedné orbity a okamžitě se objeví na jiné orbitě. Kvantový skok tedy ve skutečnosti není nějaká převratná změna, ale náhlá malá změna z jedné oblasti do druhé.

Když člověk měří nějaký proces v subatomárním měřítku a projeví se princip neurčitosti, pak lze říci, že lidská činnost ovlivnila měřenou věc. Provedení měření, jehož cílem je získat přesný údaj o poloze částice, nevyhnutelně ovlivní její hybnost a ať už je učiněno cokoli, aby se tato hybnost změřila co nejdříve po změření její polohy, pravděpodobnost toho, jaká hybnost bude zjištěna, se nemůže nezměnit. Princip neurčitosti tedy může vysvětlit některé druhy interferencí vyvolaných badateli, které ovlivňují výsledky experimentu nebo pozorování. Ne všechny efekty pozorovatele jsou však způsobeny kvantovými efekty nebo principem neurčitosti. Zbytek jsou "efekty pozorovatele", ale nikoliv kvantové efekty neurčitosti.

Pozorovací efekty zahrnují nejrůznější věci, které působí v běžném lidském měřítku událostí. Pokud se antropolog snaží získat jasnou představu o životě v primitivní společnosti, ale jeho přítomnost rozruší komunitu, kterou navštěvuje, mohou být jeho pozorování velmi zavádějící. Žádná z relevantních interakcí však neprobíhá na úrovni popsané kvantovou mechanikou nebo principem neurčitosti.

Někdy se pro reklamní účely používá slovo "kvantový", které označuje něco nového a výkonného. Například výrobce malých benzinových motorů Briggs and Stratton má jednu řadu čtyřválcových motorů s nízkým výkonem pro benzínové sekačky a podobné zahradní nářadí, kterou nazývá "Quantum".

Další čtení

• Úvod do kvantové teorie, str. 115 a 158

J.P. McEvoy a Oscar Zarate