Heisenbergův princip neurčitosti

Záměna s efektem pozorovatele

Historicky se princip neurčitosti zaměňoval s poněkud podobným efektem ve fyzice, který se nazývá efekt pozorovatele. Ten říká, že měření některých systémů nelze provést, aniž by došlo k ovlivnění těchto systémů. Heisenberg nabídl takový efekt pozorovatele na kvantové úrovni jako fyzikální "vysvětlení" kvantové neurčitosti.

Nyní je však jasné, že princip neurčitosti je vlastností všech vlnových systémů. V kvantové mechanice vzniká jednoduše díky vlnové povaze hmoty všech kvantových objektů. Princip neurčitosti tedy ve skutečnosti konstatuje základní vlastnost kvantových systémů a není výrokem o úspěšnosti pozorování současné technologie. "Měření" neznamená pouze proces, kterého se účastní fyzik-pozorovatel, ale spíše jakoukoli interakci mezi klasickými a kvantovými objekty bez ohledu na jakéhokoli pozorovatele.

Myšlenka neurčitosti

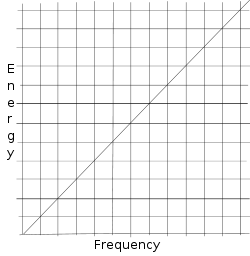
Princip neurčitosti pochází z maticové mechaniky Wernera Heisenberga. Už Max Planck věděl, že energie jednotky světla je úměrná frekvenci této jednotky světla ( E ∝ ν {\displaystyle E\propto \nu } ) a že její množství lze vyjádřit známými termíny, jako je joule, pomocí konstanty úměrnosti. Konstanta, kterou dal světu, se nyní nazývá Planckova konstanta a je reprezentována písmenem h. Když se k vyjádření kvantové mechaniky používají matice, často se musí vynásobit dvě matice, aby se získala třetí matice, která dává odpověď, kterou se fyzik snaží najít. Ale vynásobení matice, jako je P (pro hybnost), maticí, jako je X (pro polohu), dává jinou matici odpovědi, než když vynásobíte X maticí P. Výsledek vynásobení P maticí X a X maticí P a jejich následné porovnání vždy zahrnuje Planckovu konstantu jako faktor. Číslo použité pro zápis Planckovy konstanty bude vždy záviset na použitém systému měření. (Při určitém systému měření je její číselná hodnota rovna jedné.) Sklon přímky v diagramu vpravo, která znázorňuje poměr frekvence a energie, bude rovněž záviset na zvoleném systému měření.

Následující grafy ukazují, co se stane, když se pokusíme měřit polohu i hybnost.

Praktickým výsledkem tohoto matematického objevu je, že když fyzik objasní polohu, pak se hybnost stane méně jasnou, a když fyzik objasní hybnost, pak se poloha stane méně jasnou. Heisenberg říkal, že věci jsou "neurčité", a jiní lidé rádi říkali, že jsou "neurčité". Matematika však ukazuje, že právě věci ve světě jsou neurčité nebo "rozmazané", a ne že je to jen tím, že si lidé nejsou jisti tím, co se děje.

Pružinový otvor měří hybnost


Úzký otvor, rozptýlené ohnisko


Zúžením mezery se zvýší jistota, kde se foton uprostřed nachází, ale jeho směr odtamtud k detekčnímu plátnu vpravo se pak stane odpovídajícím způsobem nejistějším.


Široký otvor, ostré zaostření


Zavěšení středové mezery pomocí pružin umožňuje měřit hybnost, ale nepředvídatelně pohybuje mezerou, takže se ztrácí informace o poloze fotonu uprostřed.

Převedení neurčitosti do matematické podoby

Zde si ukážeme první rovnici, která dala základní myšlenku později zobrazenou v Heisenbergově principu neurčitosti.

Heisenberg ve svém přelomovém článku z roku 1925 nepoužívá matice a ani se o nich nezmiňuje. Heisenbergovým velkým úspěchem bylo "schéma, které bylo v principu schopné jednoznačně určit příslušné fyzikální vlastnosti (přechodové frekvence a amplitudy)" vodíkového záření.

Poté, co Heisenberg napsal svou průlomovou práci, dal ji jednomu ze svých učitelů, aby ji opravil, a odjel na dovolenou. Max Born byl zmaten rovnicemi a nekomutujícími rovnicemi, které i Heisenberg považoval za problém. Po několika dnech Born pochopil, že tyto rovnice jsou návodem k vypisování matic. Matice byly i pro tehdejší matematiky nové a zvláštní, ale jak s nimi počítat, už bylo jasně známo. Než se Heisenberg vrátil z dovolené, on a několik dalších lidí vše vypracovali v maticovém tvaru a během několika měsíců jim nová kvantová mechanika v maticovém tvaru poskytla základ pro další práci.

Max Born si všiml, že při výpočtu matic, které představují pq a qp, se tyto matice nerovnají. Totéž viděl již Heisenberg z hlediska svého původního způsobu zápisu a Heisenberg možná tušil to, co bylo Bornovi téměř okamžitě zřejmé - že rozdíl mezi maticemi odpovědí pro pq a pro qp bude vždy zahrnovat dva činitele, které vyšly z Heisenbergovy původní matematiky: Planckova konstanta h a i, což je odmocnina ze záporné jedničky. Takže samotná myšlenka toho, co Heisenberg raději nazýval "princip neurčitosti" (obvykle známý jako princip neurčitosti), se skrývala v Heisenbergových původních rovnicích.

Heisenberg se zabýval změnami, ke kterým dochází v atomu, když elektron změní svou energetickou hladinu a přiblíží se tak ke středu atomu nebo se od něj vzdálí, a zejména situacemi, kdy elektron ve dvou krocích spadne do nižšího energetického stavu. Max Born vysvětlil, jak převzal Heisenbergův podivný "recept" na zjištění součinu C nějaké změny v atomu z energetické hladiny n na energetickou hladinu n-b, který spočíval v tom, že se vzal součet násobení jedné změny něčeho, co se nazývá A (což může být například frekvence nějakého fotonu), vyvolané změnou energie elektronu v atomu mezi energetickým stavem n a energetickým stavem n-a), následnou změnou něčeho, co se nazývá B (což může být například amplituda změny), vyvolanou jinou změnou energetického stavu z n-a na n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

a objevil něco převratného:

Na základě ...příkladů... [Heisenberg] zjistil toto pravidlo..... To bylo v létě 1925. Heisenberg ... si vzal dovolenou ... a předal mi svůj článek k publikaci.....

Heisenbergovo pravidlo násobení mě nenechalo v klidu a po týdnu intenzivního přemýšlení a zkoušení jsem si náhle vzpomněl na algebraickou teorii....Takovéto čtvercové matice jsou matematikům docela známé a říká se jim matice, ve spojení s určitým pravidlem násobení. Toto pravidlo jsem aplikoval na Heisenbergovu kvantovou podmínku a zjistil jsem, že pro diagonální prvky souhlasí. Bylo snadné uhodnout, jaké musí být zbývající prvky, totiž nulové; a okamžitě přede mnou stál podivný vzorec

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
[Symbol Q je matice pro posunutí, P je matice pro hybnost, i znamená druhou odmocninu ze záporné jedničky a h je Planckova konstanta.]

Později Heisenberg svůj objev převedl do jiné matematické podoby:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Speciální symbol ℏ {\displaystyle {\hbar }} se nazývá "h-bar" nebo "redukovaná Planksova konstanta" a je roven h 2 π {\displaystyle {\frac {h}{2\pi }}} .)

Matematika je způsob, jak popsat věci, které se dějí v reálném světě. Možná si představujete, že by bylo snadné získat jak přesnou polohu něčeho, tak jeho přesnou hmotnost, dráhu a rychlost zároveň. Ve skutečnosti však musíte udělat dvě věci, abyste dostali odpověď. Pokud měříte polohu a hybnost střely, která uvízla někde ve skále velké hory, je to jednoduchá záležitost. Hora se zdánlivě nikam nepohybuje a stejně tak se nikam nepohybuje ani kulka. Její poloha je tedy známa a její rychlost je 0, takže její hybnost je také 0. Pokud se však kulka nachází někde mezi zbraní a cílem, bude obtížné zjistit její polohu v daném okamžiku. Nejlepší, co můžeme udělat, je pořídit její snímek pomocí fotoaparátu s velmi rychlou závěrkou. Jediné stisknutí závěrky by nám však dalo pouze jedinou informaci, a to polohu střely v čase t. Abychom získali hybnost, mohli bychom střelám do cesty postavit blok parafínu a změřit, jak se blok parafínu pohnul, když zastavil střelu. Nebo, pokud bychom znali hmotnost střely, mohli bychom pořídit sekvenci dvou snímků, vypočítat rychlost tak, že bychom znali rozdíl mezi dvěma polohami střely a čas mezi jejími dvěma objeveními. Ať už to uděláme jakkoli, musíme změřit hmotnost a polohu a čas mezi jednotlivými výskyty. Nakonec provedeme nejméně dvě měření, abychom se dostali k hodnotám x a p. V takovém případě musíme zvolit, které měření provedeme jako první a které jako druhé. Zdá se, že je jedno, v jakém pořadí měření provedeme. Změřit hmotnost střely a pak dvakrát změřit její polohu, nebo dvakrát změřit polohu střely a pak střelu znovu získat a změřit její hmotnost by přece nemělo žádný význam, ne? Koneckonců jsme s kulkou nic neudělali, když jsme ji vážili nebo když jsme ji fotografovali.

Na velmi malém měřítku, když měříme něco takového, jako je elektron, s ním však každé měření něco udělá. Pokud nejprve změříme polohu, změníme při tom jeho momemtum. Pokud nejprve změříme hybnost elektronu, pak v průběhu procesu změníme jeho polohu. Doufali bychom, že změříme jednu z nich a pak změříme druhou, než se něco změní, ale naše měření samo o sobě způsobí změnu a nejlepší, v co můžeme doufat, je snížit na minimum energii, kterou měřením elektronu přispíváme. Toto minimální množství energie má jako jeden z faktorů Planckovu konstantu.

Nejistota přesahuje rámec maticové matematiky

Heisenbergův princip neurčitosti byl nalezen v prvních rovnicích "nové" kvantové fyziky a teorie byla podána pomocí maticové matematiky. Princip neurčitosti je však faktem o přírodě a objevuje se i v jiných způsobech pojednání o kvantové fyzice, například v rovnicích Erwina Schrödingera.

Neurčitost v přírodě, nikoli neurčitost lidí

Na Heisenbergův objev se nahlíží dvěma různými způsoby: Někteří lidé si myslí, že věci, které se dějí v přírodě, jsou "determinované", to znamená, že se dějí podle určitého pravidla, a kdybychom mohli vědět vše, co potřebujeme vědět, mohli bychom vždy říci, co se stane příště. Jiní lidé si myslí, že věci, které se dějí v přírodě, se řídí pouze pravděpodobností a my můžeme vědět pouze to, jak se věci budou chovat v průměru - ale to víme velmi přesně.

Fyzik John Stewart Bell objevil způsob, jak dokázat, že první způsob nemůže být správný. Jeho práce se nazývá Bellova věta nebo Bellova nerovnost.

Populární kultura

Výraz "kvantový skok" nebo "kvantový skok" je chápán jako výraz pro nějakou velkou a transformační změnu a často se používá v hyperbolických vyjádřeních politiků a v prodejních kampaních v masmédiích. V kvantové mechanice se používá k popisu přechodu elektronu z jedné dráhy kolem jádra atomu na jakoukoli jinou dráhu, vyšší nebo nižší.

Někdy se slovo "quantum" používá v názvech komerčních produktů a podniků. Například společnost Briggs and Stratton vyrábí mnoho druhů malých benzinových motorů pro sekačky na trávu, rotační kypřiče a další podobné malé stroje. Jeden z jejich modelových názvů je "Quantum".

Protože princip neurčitosti říká, že určitá měření na atomární úrovni nelze provést, aniž by došlo k narušení jiných měření, někteří jedinci tuto myšlenku používají k popisu případů v lidském světě, kdy činnost pozorovatele mění sledovanou věc. Antropolog se může vydat na nějaké vzdálené místo, aby zjistil, jak tam lidé žijí, ale skutečnost, že je tam pozoruje cizí osoba z vnějšího světa, může změnit způsoby, jakými tito lidé jednají.

Věci, které lidé dělají při pozorování a které mění pozorované, jsou případy efektu pozorovatele. Některé věci, které lidé dělají, způsobují změny na velmi malé úrovni atomů a jsou případy neurčitosti nebo neurčitosti, jak je poprvé popsal Heisenberg. Princip neurčitosti ukazuje, že vždy existuje omezení, jak malé můžeme provést určité dvojice měření, například polohy a rychlosti nebo trajektorie a hybnosti. Efekt pozorovatele říká, že někdy to, co lidé dělají při pozorování věcí, např. když se dozvídají o mraveništi tím, že ho vykopou zahradním nářadím, může mít velké účinky, které změní to, co se snažili zjistit.