Tečkový součin

Definice

Tečkový součin dvou vektorů a = [a₁ , a₂ , ..., a_n ] a b = [b₁ , b₂ , ..., b_n ] je definován jako:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

kde Σ znamená součtový zápis (součet všech členů) a n je dimenze vektorového prostoru.

V dimenzi 2 je bodový součin vektorů [a,b] a [c,d] ac + bd. Stejně tak v dimenzi 3 je bodový součin vektorů [a,b,c] a [d,e,f] ad + be + cf. Například bodový součin dvou trojrozměrných vektorů [1, 3, -5] a [4, -2, -1] je následující

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Geometrická interpretace

V euklidovské geometrii spolu souvisí bodový součin, délka a úhel. Pro vektor a je tečkový součin a - a čtvercem délky a, neboli

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

kde ||a| označuje délku (velikost) a. Obecněji řečeno, je-li b jiný vektor.

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \pravý\|\cos \theta \,}

kde ||a|| a ||b| označují délky a a b a θ je úhel mezi nimi.

Tento vzorec lze upravit tak, aby určoval velikost úhlu mezi dvěma nenulovými vektory:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}\right)}

Vektory lze také nejprve převést na jednotkové vektory dělením jejich velikostí:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}

pak úhel θ je dán vztahem

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\tučný symbol {\hat {a}}}\cdot {\tučný symbol {\hat {b}}})}

Protože kosinus 90° je nulový, je bodový součin dvou kolmých vektorů vždy nulový. Kromě toho lze dva vektory považovat za ortogonální tehdy a jen tehdy, když je jejich bodový součin roven nule a oba mají nenulovou délku. Tato vlastnost poskytuje jednoduchou metodu pro testování podmínky ortogonality.

Někdy se tyto vlastnosti používají také pro definici bodového součinu, zejména ve dvou a třech rozměrech; tato definice je ekvivalentní výše uvedené definici. Pro vyšší dimenze lze vzorec použít k definici pojmu úhel.

Geometrické vlastnosti spočívají v tom, že báze je ortonormální, tj. skládá se z dvojic na sebe kolmých vektorů s jednotkovou délkou.

Skalární projekce

Pokud mají a i b délku jedna (tj. jsou to jednotkové vektory), jejich bodový součin jednoduše udává kosinus úhlu mezi nimi.

Pokud je pouze b jednotkový vektor, pak tečkový součin a - b dává |a| cos(θ), tj. velikost průmětu a do směru b, se znaménkem minus, pokud je směr opačný. Tomu se říká skalární projekce a na b nebo skalární složka a ve směru b (viz obrázek). Tato vlastnost bodového součinu má několik užitečných aplikací (viz například další část).

Pokud a ani b není jednotkový vektor, pak velikost průmětu a ve směru b bude například a - (b / |b|), protože jednotkový vektor ve směru b je b / |b|.

Rotace

Rotace ortonormální báze, v níž je reprezentován vektor a, se získá násobením a maticí rotace R. Toto násobení matic je pouze kompaktní reprezentací posloupnosti bodových součinů.

Nechte například

• B₁ = {x, y, z} a B₂ = {u, v, w} jsou dvě různé ortonormální báze téhož prostoru R³ , přičemž B₂ získáme pouhým otočením B₁ ,
• a₁ = (a_x , a_y , a_z ) představují vektor a ve smyslu B₁ ,
• a₂ = (a_u , a_v , a_w ) představují stejný vektor z hlediska otočeného základu B₂ ,
• u₁ , v₁ , w₁ jsou pootočené bázové vektory u, v, w reprezentované v termínech B₁ .

Poté se provede rotace z B₁ do B₂ takto:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}. }

Všimněte si, že rotační matice R je sestavena tak, že jako její řádky jsou použity rotované bázové vektory u₁ , v₁ , w₁ a tyto vektory jsou jednotkové vektory. Podle definice se Ra₁ skládá z posloupnosti bodových součinů mezi každým ze tří řádků R a vektorem a₁ . Každý z těchto bodových součinů určuje skalární složku a ve směru otočeného bázového vektoru (viz předchozí část).

Pokud je₁ řádkový vektor, nikoliv sloupcový, pak R musí obsahovat otočené bázové vektory ve svých sloupcích a musí dodatečně vynásobit a₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

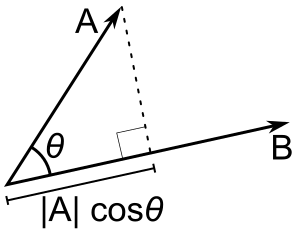
A - B = |A| |B| cos(θ). |A| cos(θ) je skalární projekce A na B.

Fyzika

Ve fyzice je magnituda skalár ve fyzikálním smyslu, tj. fyzikální veličina nezávislá na souřadnicovém systému, vyjádřená jako součin číselné hodnoty a fyzikální jednotky, nikoliv pouze číslo. Bodový součin je v tomto smyslu také skalár, daný vzorcem, nezávislý na souřadnicovém systému. Příklad:

• Mechanická práce je tečkovým součinem vektorů síly a posunutí.
• Magnetický tok je tečkovým součinem magnetického pole a plošných vektorů.
• Objemový průtok je tečkovým součinem vektorů rychlosti kapaliny a plochy.

Vlastnosti

Pokud jsou a, b a c reálné vektory a r je skalár, platí následující vlastnosti.

Tečkový součin je komutativní:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Tečkový součin je distributivní nad sčítáním vektorů:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Bodový součin je bilineární:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Při násobení skalární hodnotou splňuje bodový součin následující podmínky:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(tyto dvě poslední vlastnosti vyplývají z prvních dvou).

Dva nenulové vektory a a b jsou kolmé tehdy a jen tehdy, když a - b = 0.

Na rozdíl od násobení obyčejných čísel, kde platí, že pokud ab = ac, pak se b vždy rovná c, pokud a není rovno nule, u tečkového součinu neplatí zákon zrušení:

Jestliže a - b = a - c a a ≠ 0, pak podle distributivního zákona můžeme napsat: a - (b - c) = 0; výše uvedený výsledek říká, že to znamená pouze to, že a je kolmé na (b - c), což stále umožňuje (b - c) ≠ 0, a tedy b ≠ c.

Za předpokladu, že báze je ortonormální, je bodový součin invariantní při izometrických změnách báze: otáčení, odrazu a kombinaci, přičemž počátek zůstává pevný. Výše uvedená geometrická interpretace se o tuto vlastnost opírá. Jinými slovy, pro ortonormální prostor s libovolným počtem dimenzí je bodový součin invariantní při transformaci souřadnic na základě ortogonální matice. Tomu odpovídají následující dvě podmínky:

• Nová báze je opět ortonormální (tj. je ortonormální vyjádřená ve staré bázi).
• Nové bázové vektory mají stejnou délku jako staré (tj. jednotkovou délku z hlediska staré báze).

Jsou-li a a b funkce, pak derivace a - b je a' - b + a - b'.

Rozšíření trojitého produktu

Jedná se o velmi užitečnou identitu (známou také jako Lagrangeův vzorec) zahrnující tečkový a křížový součin. Zapisuje se jako

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

což je snazší si zapamatovat jako "BAC minus CAB", přičemž je třeba mít na paměti, které vektory jsou tečkované. Tento vzorec se běžně používá pro zjednodušení vektorových výpočtů ve fyzice.

Důkaz geometrické interpretace

Uvažujme prvek R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}}. _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Opakovaným použitím Pythagorovy věty získáme pro její délku |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Ale to je totéž jako

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

z toho vyplývá, že když vektor v vynásobíme tečkovým součinem se sebou samým, dostaneme délku vektoru ve čtverci.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Nyní uvažujme dva vektory a a b vycházející z počátku a oddělené od sebe úhlem θ. Třetí vektor c lze definovat jako

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\\ \mathbf {a} -\mathbf {b} .\,}

a vytvoříme trojúhelník o stranách a, b a c. Podle zákona kosinusů máme následující vztahy

| c | 2 = | a | 2 + | b | 2 - 2 | a | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Nahrazením tečkových součinů za čtvercové délky podle lemmatu 1 dostaneme.

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} (1)

Ale protože c ≡ a - b, máme také

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

který se podle distribučního zákona rozšíří na

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

Sloučením dvou rovnic c - c, (1) a (2), získáme následující výsledek

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Odečtením a - a + b - b od obou stran a vydělením -2 získáme následující výsledek

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Zobecnění

Vnitřní součin zobecňuje tečkový součin na abstraktní vektorové prostory a obvykle se značí ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . Díky geometrické interpretaci bodového součinu je norma ||a|| vektoru a v takovém prostoru vnitřního součinu definována jako

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

tak, že zobecňuje délku, a úhel θ mezi dvěma vektory a a b pomocí

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}. }

Zejména dva vektory jsou považovány za ortogonální, pokud je jejich vnitřní součin roven nule.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Pro vektory s komplexními vstupy by použití dané definice bodového součinu vedlo ke zcela odlišným geometrickým vlastnostem. Například tečkový součin vektoru se sebou samým může být libovolné komplexní číslo a může být nulový, aniž by vektor byl nulovým vektorem; to by zase mělo závažné důsledky pro pojmy jako délka a úhel. Mnoho geometrických vlastností lze zachránit, i když za cenu vzdání se symetrických a bilineárních vlastností skalárního součinu, alternativní definicí

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

kde b_i je komplexní konjugát b_i . Pak skalární součin libovolného vektoru se sebou samým je nezáporné reálné číslo a je nenulový s výjimkou nulového vektoru. Tento skalární součin však není lineární v b (ale spíše konjugovaný lineární) a skalární součin není ani symetrický, protože

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} .

Tento typ skalárního součinu je nicméně docela užitečný a vede k pojmům hermitovské formy a obecného vnitřního součinového prostoru.

Frobeniův vnitřní součin zobecňuje tečkový součin na matice. Je definován jako součet součinů příslušných složek dvou matic stejné velikosti.

Zobecnění na tenzory

Tečkový součin mezi tenzorem řádu n a tenzorem řádu m je tenzor řádu n+m-2. Tečkový součin se vypočítá vynásobením a sečtením přes jeden index v obou tenzorech. Jestliže A {\displaystyle \mathbf {A} } a B {\displaystyle \mathbf {B}. } jsou dva tenzory se zastoupením prvků A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} a B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} prvky bodového součinu A ⋅ B {\displaystyle \mathbf {A}. \cdot \mathbf {B} } jsou dány vztahem

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

Tato definice se přirozeně redukuje na standardní vektorový bodový součin, pokud se aplikuje na vektory, a na maticové násobení, pokud se aplikuje na matice.

Příležitostně se používá dvojnásobný tečkový součin, který vyjadřuje násobení a sčítání přes dva indexy. Dvojitý bodový součin dvou tenzorů 2. řádu je skalár.

Související stránky

• Cauchyho-Schwarzova nerovnost
• Křížový produkt
• Násobení matic
• Fyzika