Vennův diagram
Vennův diagram je diagram, který znázorňuje logický vztah mezi množinami. Zpopularizoval je John Venn v 80. letech 19. století a dnes se hojně používají. Používají se při výuce elementární teorie množin a k ilustraci jednoduchých množinových vztahů v pravděpodobnosti, logice, statistice, lingvistice a informatice. Vennův diagram používá k znázornění množin uzavřené křivky nakreslené v rovině. Velmi často jsou to kružnice nebo elipsy.
Podobné myšlenky byly navrženy již před Vennem. Christian Weise v roce 1712 (Nucleus Logicoe Wiesianoe) a Leonhard Euler (Dopisy německé princezně) 1768 přišli s podobnými myšlenkami. Myšlenku zpopularizoval Venn v Symbolické logice, kapitola V "Diagramatická reprezentace", 1881.

Vitráž v Cambridge, kde John Venn studoval. Zobrazuje Vennův diagram.
Příklad
Následující příklad používá dvě sady, A a B, které jsou zde znázorněny barevnými kroužky. Oranžový kruh, množina A, představuje všechny dvounohé živé tvory. Modrý kruh, sada B, představuje živé tvory, kteří mohou létat. Každý samostatný typ tvora si lze představit jako bod někde v diagramu. Živí tvorové, kteří mohou létat a zároveň mají dvě nohy - například papoušci - jsou pak v obou sadách, takže odpovídají bodům v oblasti, kde se modré a oranžové kruhy překrývají. Tato oblast obsahuje všechny takové a pouze takové živé tvory.
Lidé a tučňáci jsou dvounozí, a proto jsou pak v oranžovém kruhu, ale protože nemohou létat, objevují se v levé části oranžového kruhu, kde se nepřekrývá s modrým kruhem. Komáři mají šest nohou a létají, takže bod pro komáry je v části modrého kruhu, která se nepřekrývá s oranžovým. Tvorové, kteří nemají dvě nohy a nemohou létat (například velryby a pavouci), by byli všichni zastoupeni body mimo oba kruhy.
Spojená plocha množin A a B se nazývá sjednocení A a B, označuje se A ∪ B. Sjednocení v tomto případě obsahuje všechny živé tvory, kteří jsou buď dvounozí, nebo mohou létat (nebo obojí). Oblast v A i B, kde se obě množiny překrývají, se nazývá průnik A a B, označuje se A ∩ B. Například průnik obou množin není prázdný, protože existují body, které představují tvory, kteří jsou v oranžovém i modrém kruhu.
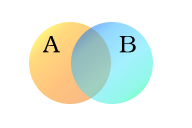
Sady A (dvounohá zvířata) a B (zvířata, která mohou létat).
Otázky a odpovědi
Otázka: Co je to Vennův diagram?
Odpověď: Vennův diagram je diagram, který znázorňuje logický vztah mezi množinami. K znázornění množin používá uzavřené křivky nakreslené v rovině, obvykle kružnice nebo elipsy.
Otázka: Kdo zpopularizoval Vennovy diagramy?
Odpověď: John Venn zpopularizoval Vennovy diagramy v 80. letech 19. století.
Otázka: K čemu se používají?
Odpověď: Používají se k výuce základní teorie množin a k znázornění jednoduchých množinových vztahů v pravděpodobnosti, logice, statistice, lingvistice a informatice.
Otázka: Kdo navrhl podobné myšlenky před Johnem Vennem?
Odpověď: Podobné myšlenky navrhl Christian Weise v roce 1712 ve svém díle Nucleus Logicoe Wiesianoe a Leonhard Euler je navrhl v Dopisech německé princezně v roce 1768.
Otázka: Kdy John Venn publikoval Symbolickou logiku?
Odpověď: John Venn vydal Symbolickou logiku v roce 1881.
Otázka: Ve které kapitole Symbolické logiky John Venn zpopularizoval myšlenku Vennova diagramu?
Odpověď: Myšlenku Vennova diagramu zpopularizoval John Venn v kapitole 5 "Diagramatická reprezentace" knihy Symbolická logika.
Otázka: Jak byly tyto myšlenky reprezentovány před vynálezem moderní verze Vennova diagramu?
O: Před vynálezem moderní verze Vennova diagramu byly tyto myšlenky znázorňovány pomocí uzavřených křivek nakreslených v rovině, jako jsou kružnice nebo elipsy.
Vyhledávání