Logaritmická stupnice
Logaritmická stupnice je stupnice používaná v případě velkého rozsahu veličin. Běžně se používá například pro sílu zemětřesení, hlasitost zvuku, intenzitu světla nebo pH roztoků.
Je založena na řádových hodnotách, nikoli na standardní lineární stupnici. Hodnota každé značky na stupnici je hodnota předchozí značky vynásobená konstantou.
Logaritmické stupnice se používají také v posuvných měřítkách pro násobení nebo dělení čísel sčítáním nebo odčítáním délek na stupnicích.
Logaritmická stupnice může být užitečná v případě, že data pokrývají velký rozsah hodnot - logaritmus je redukuje na lépe zvládnutelný rozsah.
Některé naše smysly fungují logaritmicky (násobením skutečné síly vstupního signálu se k síle vnímaného signálu přičítá konstanta, viz: Stevensův mocninný zákon). Proto jsou logaritmické stupnice pro tyto vstupní veličiny obzvláště vhodné. Zejména náš sluch vnímá stejné násobky frekvencí jako stejné rozdíly ve výšce tónu.
Na většině logaritmických stupnic odpovídají malé násobky (nebo poměry) základní veličiny malým (případně záporným) hodnotám logaritmické míry.
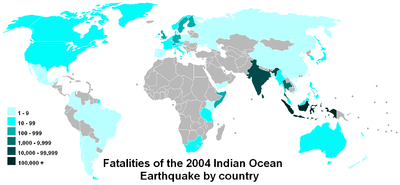
Logaritmické měřítko usnadňuje porovnávání hodnot, které pokrývají velký rozsah, jako například na této mapě.
Dvě logaritmické stupnice posuvného pravítka
Příklady
Známými příklady takových vah jsou:
- Richterova stupnice a momentová stupnice (MMS) pro sílu zemětřesení a pohyby v zemi.
- bel a decibel a neper pro akustický výkon (hlasitost) a elektrický výkon;
- počítání f-stopů pro poměry fotografické expozice;
- ohodnocení nízkých pravděpodobností počtem "devítek" v desetinném rozkladu pravděpodobnosti, že nenastanou: například systém, který selže s pravděpodobností 10−5je spolehlivý na 99,999 %: "pět devítek".
- Entropie v termodynamice.
- Informace v teorii informace.
- Křivky distribuce velikosti částic v půdě
Některé logaritmické stupnice byly navrženy tak, že velkým hodnotám (nebo poměrům) základní veličiny odpovídají malé hodnoty logaritmické míry. Příklady takových stupnic jsou:
- pH pro kyselost;
- stupnice hvězdné velikosti pro jasnost hvězd;
Logaritmická stupnice je také grafická stupnice na jedné nebo obou stranách grafu, kde je číslo x vytištěno ve vzdálenosti c-log(x) od bodu označeného číslem 1. Pravítko má logaritmické stupnice a nomogramy často používají logaritmické stupnice. Na logaritmické stupnici je stejný řádový rozdíl reprezentován stejnou vzdáleností. Geometrický průměr dvou čísel je uprostřed mezi těmito čísly.
Logaritmický grafický papír byl před nástupem počítačové grafiky základním vědeckým nástrojem. Grafy na papíře s jednou logaritmickou stupnicí mohou zobrazovat exponenciální zákony a na logaritmickém papíře mocninné zákony jako přímky (viz semilogový graf, logaritmický graf).
Otázky a odpovědi
Otázka: Co je to logaritmická stupnice?
Odpověď: Logaritmická stupnice je stupnice, která se používá při velkém rozsahu veličin.
Otázka: Jaké jsou příklady věcí, které lze měřit na logaritmické stupnici?
Odpověď: Na logaritmické stupnici lze měřit sílu zemětřesení, hlasitost zvuku, intenzitu světla, rychlost šíření epidemií a pH roztoků.
Otázka: Jak se logaritmická stupnice liší od standardní lineární stupnice?
Odpověď: Logaritmická stupnice je založena na řádových hodnotách, nikoli na standardní lineární stupnici. Hodnota každé značky na stupnici je hodnota předchozí značky vynásobená konstantou.
Otázka: Jaká je výhoda používání logaritmické stupnice?
Odpověď: Logaritmická stupnice dokáže zmenšit velký rozsah hodnot na lépe zvládnutelný rozsah, což může být užitečné při práci s daty, která zahrnují široký rozsah hodnot.
Otázka: Co je Stevensův mocninný zákon a jak souvisí s logaritmickými stupnicemi?
Odpověď: Stevensův mocninný zákon popisuje, jak některé naše smysly fungují logaritmickým způsobem, kdy se násobením skutečné vstupní síly přičítá k vnímané síle signálu konstanta. Proto jsou logaritmické stupnice pro tyto vstupní veličiny obzvláště vhodné.
Otázka: Proč je logaritmická stupnice obzvláště užitečná pro měření hlasitosti zvuku?
Odpověď: Náš sluch vnímá stejné násobky frekvencí jako stejné rozdíly ve výšce tónu, takže logaritmická stupnice může přesně vyjádřit tento vztah mezi frekvencí zvuku a vnímanou hlasitostí.
Otázka: Jaký je vztah mezi malými násobky základní veličiny a logaritmickou mírou na většině logaritmických stupnic?
Odpověď: Na většině logaritmických stupnic odpovídají malé násobky (nebo poměry) základní veličiny malým (případně záporným) hodnotám logaritmické míry.
Vyhledávání