Diferenciální počet

Pozadí

Na rozdíl od čísla, jako je 5 nebo 200, může proměnná měnit svou hodnotu. Například vzdálenost a čas jsou proměnné. Při olympijském běžeckém závodě se s tím, jak člověk běží, zvyšuje jeho vzdálenost od startovní čáry. Mezitím stopky nebo hodiny měří čas, který se zvyšuje. Průměrnou rychlost běžce můžeme změřit, když vzdálenost, kterou uběhl, vydělíme časem, který mu k tomu stačil. To však nevypovídá o tom, jakou rychlostí dotyčný běžel přesně 1,5 sekundy po doběhu. Kdybychom měli vzdálenost po 1 sekundě a vzdálenost po 2 sekundách, stále bychom měli pouze průměr, i když by byl pravděpodobně správnější než průměr za celý závod.

Dokud nebyl vynalezen kalkul, jediným způsobem, jak to zjistit, bylo rozřezat čas na menší a menší části, takže průměrná rychlost za menší čas se stále více blížila skutečné rychlosti přesně 1,5 sekundy. Tento postup byl velmi zdlouhavý a náročný a musel se provádět pokaždé, když lidé chtěli něco vyřešit. Představte si řidiče, který se snaží zjistit rychlost auta pouze pomocí jeho počítadla kilometrů (měřiče vzdálenosti) a hodin, bez tachometru!

Velmi podobným problémem je nalezení sklonu (strmosti) v libovolném bodě křivky. Sklon přímky se dá snadno určit - je to jednoduše to, o kolik stoupá (y neboli svislice) děleno tím, o kolik jde napříč (x neboli vodorovná rovina). Pokud je přímka rovnoběžná s osou x, pak je její sklon nulový. Pokud přímka procházela body (x,y) = (2,10) a (4,18), pak přímka stoupá nahoru o 8 a jde napříč o 2, takže její sklon je 8 děleno 2, což je 4.

Na "křivce" je však sklon proměnný (má v různých bodech různé hodnoty), protože přímka se ohýbá. Kdybychom však křivku rozřezali na velmi, velmi malé kousky, křivka by v daném bodě vypadala téměř jako velmi krátká přímka. Abychom tedy zjistili její sklon, můžeme bodem protáhnout přímku se stejným sklonem, jaký má křivka v tomto bodě. Pokud je to provedeno přesně, bude mít přímka stejný sklon jako křivka a nazývá se tečna. Neexistuje však žádný způsob, jak zjistit (bez výpočtu), zda je tečna přesně správná, a naše oči nejsou dostatečně přesné, abychom si mohli být jisti, zda je přesná, nebo jen velmi blízká.

Newton a Leibniz našli způsob, jak přesně určit sklon (nebo rychlost v příkladu se vzdáleností) pomocí jednoduchých a logických pravidel. Rozdělili křivku na nekonečný počet velmi malých částí. Poté si vybrali body na obou stranách bodu, který je zajímal, a u každého z nich vypočítali tečnu. Jak se body přibližovaly k bodu, který je zajímal, sklon se blížil určité hodnotě, protože tečny se blížily skutečnému sklonu křivky. Řekli, že tato konkrétní hodnota, ke které se blíží, je skutečný sklon.

 
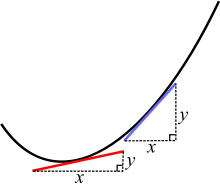
Na křivce mají dva různé body různý sklon. Červená a modrá čára jsou tečny ke křivce.  

Jak to funguje

Řekněme, že máme funkci y = f(x). f je zkratka pro funkci, takže tato rovnice znamená "y je funkcí x". To nám říká, že to, jak vysoko je y na svislé ose, závisí na tom, jaké je v daném okamžiku x (vodorovná osa). Například u rovnice y = x² víme, že pokud je x 1, pak y bude 1; pokud je x 3, pak y bude 9; pokud je x 20, pak y bude 400.

Zvolte si na křivce bod A a jeho vodorovnou polohu nazvěte x. Pak si zvolte na křivce jiný bod B, který je o něco dále napříč než A, a jeho vodorovnou polohu nazvěte x + h. Na velikosti h nezáleží, je to velmi malé číslo.

Když tedy přejdeme z bodu A do bodu B, svislá poloha se změní z f(x) na f(x + h) a vodorovná poloha se změní z x na x + h. Nyní si pamatujte, že sklon je děleno, o kolik stoupá nahoru a o kolik jde napříč. Sklon tedy bude:

f ( x + h ) - f ( x ) h {\displaystyle {\frac {f(x+h)-f(x)}{h}}}

Přibližujeme-li B stále více k bodu A, což znamená, že h se stále více blíží nule, pak se blížíme k tomu, abychom věděli, jaký je sklon v bodě A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}}

Nyní se vraťme k y = x². Její sklon můžeme určit takto:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}}\end{aligned}}}}

Použitím binomické věty, která říká ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}} , můžeme redukovat na:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\&=\lim _{h\rightarrow 0}2x+h\&={\frac {}{}}2x\{end{aligned}}}

Víme tedy, aniž bychom museli kreslit tečné čáry, že v každém bodě křivky f(x) = x² bude derivace f'(x) (označená apostrofem) v každém bodě rovna 2x. Tomuto postupu, při kterém se pomocí limit určuje sklon, se říká diferenciace neboli nalezení derivace.

Leibniz došel ke stejnému výsledku, ale nazval h "dx", což znamená "malá část x". Výslednou změnu f(x) nazval "dy", což znamená "nepatrné množství y". Leibnizův zápis se používá ve více knihách, protože je snadno pochopitelný, když se rovnice stanou složitějšími. V Leibnizově notaci:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}=f'(x)}

 
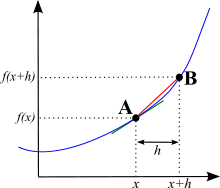
Obrázek znázorňující, co na křivce znamená x a x + h.  

Pravidla

Pomocí výše uvedeného systému matematici vypracovali pravidla, která fungují vždy, bez ohledu na to, o jakou funkci se jedná. (Poznámka: zde u {\displaystyle u} a v {\displaystyle v} jsou obě funkce x {\displaystyle x} ).

Stav	Funkce	Derivát	Příklad	Derivát
Číslo samo o sobě	y = a {\displaystyle y=a}	d y d x = 0 {\displaystyle {\frac {dy}{dx}}=0}	y = 3 {\displaystyle y=3}	0 {\displaystyle 0}
Přímka	y = m x + c {\displaystyle y=mx+c}	d y d x = m {\displaystyle {\frac {dy}{dx}}=m}	y = 3 x + 5 {\displaystyle y=3x+5}	3 {\displaystyle 3}
x na mocninu čísla	x a {\displaystyle x^{a}}	d y d x = a x a - 1 {\displaystyle {\frac {dy}{dx}}=ax^{a-1}}	x 12 {\displaystyle x^{12}}	12 x 11 {\displaystyle 12x^{11}}
Číslo vynásobené funkcí	y = c ⋅ u {\displaystyle y=c\cdot u}	d y d x = c d u d x {\displaystyle {\frac {dy}{dx}}=c{\frac {du}{dx}}}	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)}	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)}
Funkce plus další funkce	y = u + v {\displaystyle y=u+v}	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}}}	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\sqrt {x}}}	6 x + 1 x {\displaystyle 6x+{\frac {1}{\sqrt {x}}}}
Funkce minus jiná funkce	y = u - v {\displaystyle y=u-v}	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}})	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}}	6 x - 1 x {\displaystyle 6x-{\frac {1}{\sqrt {x}}}}
Pravidlo součinu  Funkce vynásobená jinou funkcí	y = u ⋅ v {\displaystyle y=u\cdot v}	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}})	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)}	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)}
Pravidlo kvocientu  Funkce dělená jinou funkcí	y = u v {\displaystyle y={\frac {u}{v}}}	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}}	y = x 2 + 2 x - 1 {\displaystyle y={\frac {x^{2}+2}{x-1}}}	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}}
Řetězové pravidlo  Používá se pro složené funkce	y = u ∘ v {\displaystyle y=u\circ v}	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}})	y = 2 x - 1 {\displaystyle y={\sqrt {2x-1}}}	2 2 2 x - 1 = 1 2 x - 1 {\displaystyle {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}}
Exponenciální funkce	y = e x {\displaystyle {\frac {}{}}y=e^{x}}	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}}	y = e x {\displaystyle {\frac {}{}}y=e^{x}}	e x {\displaystyle {\frac {}{}}e^{x}}