Gumbelovo rozdělení
Gumbelovo rozdělení je rozdělení pravděpodobnosti extrémních hodnot.
V teorii pravděpodobnosti a statistice se Gumbelovo rozdělení používá k modelování rozdělení maxima (nebo minima) určitého počtu vzorků různých rozdělení.
Takové rozdělení by mohlo být použito k vyjádření rozdělení maximální hladiny řeky v určitém roce, pokud by existoval seznam maximálních hodnot za posledních deset let. Je také užitečné při předpovídání pravděpodobnosti výskytu extrémního zemětřesení, povodně nebo jiné přírodní katastrofy.
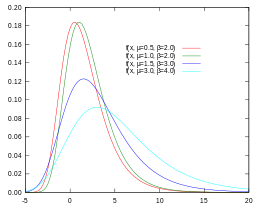
Gumbelova distribuční funkce pravděpodobnosti (PDF)
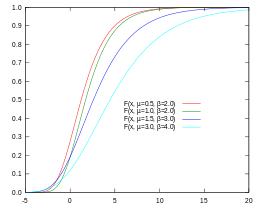
Gumbelova kumulativní distribuční funkce (CDF)
Vlastnosti
Gumbelovo rozdělení je spojité rozdělení pravděpodobnosti. Gumbelova rozdělení jsou rodinou rozdělení stejného obecného tvaru. Tato rozdělení se liší svými parametry polohy a měřítka: střední hodnota ("průměr") rozdělení určuje jeho polohu a směrodatná odchylka ("variabilita") určuje měřítko.
Rozpoznává se Gumbelova funkce hustoty pravděpodobnosti (PDF) a Gumbelova kumulativní distribuční funkce (CDF).
Pravděpodobnost P výskytu hodnoty V mezi mezními hodnotami A a B, stručně zapsaná jako P(A<V<B), se v PDF zjistí pomocí plochy pod křivkou PDF mezi A a B.
| Příklad pravděpodobnosti v PDF |
| Na obrázku normální funkce hustoty pravděpodobnosti by hodnoty na vodorovné ose měly znít: μ-3σ, μ-2σ, μ-1σ, μ+1σ, μ+2σ a μ+3σ. μ = průměr, σ = směrodatná odchylka. |
Na rozdíl od normálního rozdělení je Gumbelovo PDF a-symetrické a vychýlené doprava.
CDF
V CDF se pravděpodobnost, že hodnota V je menší než A, zjistí přímo jako hodnota CDF v bodě A:
P ( V ≤ A ) = C D F ( A ) {\displaystyle P(V\leq A)=CDF(A)}
| Příklad pravděpodobnosti v CDF |
| Na obrázku Gumbelova CDF červená křivka naznačuje, že pravděpodobnost, že V bude menší než 5, je 0,9 (neboli 90 %), zatímco u tmavě modré čáry je tato pravděpodobnost 0,7 neboli 70 %. |

Normální funkce hustoty pravděpodobnosti (PDF) je symetrická.
Matematika
CDF
Matematické vyjádření CDF je:
C D F ( A ) = e - e - ( A - μ ) / β , {\displaystyle CDF(A)=e^{-e^{-(A-\mu )/\beta }},}
kde μ je modus (hodnota, kde funkce hustoty pravděpodobnosti dosahuje svého vrcholu), e je matematická konstanta, přibližně 2,718, a β je hodnota související se směrodatnou odchylkou (σ) :
β = σ 6 / π , {\displaystyle \beta =\sigma {\sqrt {6}}/\pi ,}
kde π je řecký symbol pro číslo pí, jehož hodnota se blíží 22/7 neboli 3,142, a symbol {\displaystyle {\sqrt {\,\,}}} znamená 
Mód a medián
Modus μ lze zjistit z mediánu M, což je hodnota A, kde CDF(A)=0,5, a β:
μ = M + β ln ( ln 2 ) , {\displaystyle \mu =M+\beta \ln \left(\ln 2\right),}
kde ln je přirozený logaritmus.
Průměr
Střední hodnota E(x) je dána vztahem:
E ( x ) = μ + c β , {\displaystyle \operatorname {E} (x)=\mu +c\beta ,}
kde c {\displaystyle c}

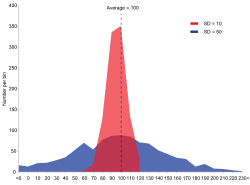
Existují dvě datové řady: červená a modrá. Obě mají stejný průměr : 100, ale modrá skupina má větší směrodatnou odchylku (SD=σ=50) než červená skupina (SD=σ=10).
Odhad
V datové řadě lze parametry modus (μ) a β odhadnout z průměru, mediánu a směrodatné odchylky. Výpočet posledních tří veličin je vysvětlen na příslušných stránkách Wiki. Poté lze pomocí vzorců uvedených v předchozí části vypočítat faktory μ a β. Tímto způsobem lze určit CDF Gumbelova rozdělení náležejícího datům a zjistit pravděpodobnost zajímavých hodnot dat.

Fitované kumulativní Gumbelovo rozdělení na maximální jednodenní říjnové srážky pomocí CumFreq
Aplikace
V hydrologii se Gumbelovo rozdělení používá k analýze takových veličin, jako jsou měsíční a roční maximální hodnoty denních srážek a objemů říčních průtoků, a také k popisu sucha.
Modrý obrázek znázorňuje příklad dosazení Gumbelova rozdělení na maximální jednodenní říjnové srážky, na kterém je znázorněn také 90% pás spolehlivosti založený na binomickém rozdělení.
Otázky a odpovědi
Otázka: Co je Gumbelovo rozdělení?
Odpověď: Gumbelovo rozdělení je pravděpodobnostní rozdělení extrémních hodnot.
Otázka: K čemu se Gumbelovo rozdělení používá?
Odpověď: Gumbelovo rozdělení se používá k modelování rozdělení maxima (nebo minima) určitého počtu vzorků různých rozdělení.
Otázka: Jak lze Gumbelovo rozdělení využít při předpovídání přírodních katastrof?
Odpověď: Gumbelovo rozdělení je užitečné při předpovídání pravděpodobnosti výskytu extrémního zemětřesení, povodně nebo jiné přírodní katastrofy.
Otázka: Jaký je příklad použití Gumbelova rozdělení k zobrazení minulé události?
Odpověď: Gumbelovo rozdělení by se dalo použít k zobrazení rozdělení maximální hladiny řeky v určitém roce, pokud by existoval seznam maximálních hodnot za posledních deset let.
Otázka: Je Gumbelovo rozdělení užitečné pouze při předpovídání přírodních katastrof?
Odpověď: Ne, Gumbelovo rozdělení lze použít k modelování rozdělení extrémních hodnot v jakékoli situaci.
Otázka: Lze Gumbelovo rozdělení použít k modelování minimální hodnoty souboru vzorků?
Odpověď: Ano, Gumbelovo rozdělení lze použít k modelování rozdělení maximální nebo minimální hodnoty souboru vzorků.
Otázka: Je Gumbelovo rozdělení běžně používaným rozdělením v teorii pravděpodobnosti a statistice?
Odpověď: Ano, Gumbelovo rozdělení je běžně používané rozdělení v teorii pravděpodobnosti a statistice, zejména pro modelování extrémních hodnot.
Vyhledávání



