Směrodatná odchylka
Směrodatná odchylka je číslo, které udává, jak jsou naměřené hodnoty pro danou skupinu rozptýleny od průměru (střední hodnoty) nebo očekávané hodnoty. Nízká směrodatná odchylka znamená, že většina čísel se blíží průměru. Vysoká směrodatná odchylka znamená, že čísla jsou více rozptýlena.
Uváděné rozpětí chyby je obvykle dvojnásobek směrodatné odchylky. Vědci běžně uvádějí směrodatnou odchylku čísel od průměrného čísla při experimentech. Často se rozhodnou, že důležité jsou pouze rozdíly větší než dvojnásobek nebo trojnásobek směrodatné odchylky. Směrodatná odchylka je užitečná také v peněžnictví, kde směrodatná odchylka u vydělaných úroků ukazuje, jak se mohou lišit vydělané úroky jedné osoby od průměru.
Mnohdy lze měřit pouze vzorek nebo část skupiny. Pak lze číslo blízké směrodatné odchylce pro celou skupinu zjistit pomocí poněkud odlišné rovnice zvané výběrová směrodatná odchylka, která je vysvětlena níže.
.png)
Graf normálního rozdělení (nebo zvonové křivky). Každý barevný pás má šířku jedné směrodatné odchylky.
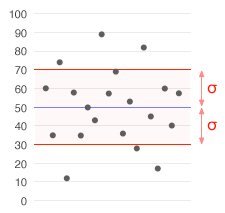
Soubor dat s průměrnou hodnotou 50 (zobrazeno modře) a směrodatnou odchylkou (σ) 20.
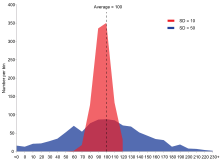
Příklad dvou výběrových souborů se stejným průměrem a různými směrodatnými odchylkami. Červená populace má průměr 100 a SD 10; modrá populace má průměr 100 a SD 50.
Základní příklad
Uvažujme skupinu, která má následujících osm čísel:
2 , 4, 4,4 , 5, , 5, 7{\displaystyle9 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9}
Těchto osm čísel má průměrnou hodnotu 5:
2 + +4 +4 +4 + + 5+ 57= 98{\displaystyle5 {\frac {2+4+4+4+5+5+7+9}{8}}=5}
Chcete-li vypočítat směrodatnou odchylku populace, zjistěte nejprve rozdíl každého čísla v seznamu od průměru. Poté výsledek každého rozdílu odmocněte:
(2 - 5) =2 ( - 3) =2 ( 95- 5) =2 = 02( 04-5 ) =2 ( - 1) =2 (15 - 5) = 2= 02( 04-5 ) = ( - ) = 2( - 1) = 2(17 - 5) =2 = 22( 44-5 ) = 2( -1 ) =2 ( 19- 5) = 2= 42{\displaystyle16 {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Dále zjistěte průměr těchto hodnot (součet dělený počtem čísel). Nakonec odečtěte druhou odmocninu:
( +9 +1 +1 +1 + 0+ 0+ 4) 16= 8{\displaystyle2 {\sqrt {\frac {(9+1+1+1+1+0+0+0+4+16)}{8}}}=2}
Odpovědí je směrodatná odchylka populace. Vzorec je pravdivý pouze v případě, že osm čísel, s nimiž jsme začali, je celá skupina. Pokud jsou pouze částí náhodně vybrané skupiny, pak bychom měli ve spodní části (jmenovateli) předposledního kroku použít číslo 7 (což je n - 1) místo čísla 8 (což je n). Pak je odpovědí výběrová směrodatná odchylka. Tomu se říká Besselova korekce.
Další příklady
Trochu těžší příklad ze života: Průměrná výška dospělých mužů ve Spojených státech je 70" se směrodatnou odchylkou 3". Směrodatná odchylka 3" znamená, že většina mužů (asi 68 %, za předpokladu normálního rozdělení) má výšku o 3" vyšší až 3" nižší než průměr (67"-73") - tedy jednu směrodatnou odchylku. Téměř všichni muži (přibližně 95 %) mají výšku o 6" vyšší až 6" nižší než průměr (64"-76") - dvě směrodatné odchylky. Tři směrodatné odchylky zahrnují všechna čísla pro 99,7 % zkoumaného vzorku populace. To platí, pokud je rozdělení normální (zvonovitého tvaru).
Kdyby byla směrodatná odchylka nulová, pak by všichni muži měřili přesně 70". Pokud by směrodatná odchylka byla 20", pak by někteří muži byli mnohem vyšší nebo mnohem nižší než průměr, s typickým rozmezím asi 50"-90".
Jiný příklad: Každá ze tří skupin {0, 0, 14, 14}, {0, 6, 8, 14} a {6, 6, 8, 8} má průměr (průměr) 7. Jejich směrodatné odchylky jsou však 7, 5 a 1. Třetí skupina má mnohem menší směrodatnou odchylku než ostatní dvě, protože všechna její čísla jsou blízká 7. Protože se v této skupině vyskytují čísla, která se blíží 7, je její směrodatná odchylka mnohem menší. Základní myšlenka je, že směrodatná odchylka nám říká, jak daleko od průměru mají ostatní čísla tendenci být. Bude mít stejné jednotky jako samotná čísla. Pokud například skupina {0, 6, 8, 14} představuje věk skupiny čtyř bratrů v letech, průměr je 7 let a směrodatná odchylka 5 let.
Směrodatná odchylka může sloužit jako míra nejistoty. Například ve vědě pomáhá směrodatná odchylka skupiny opakovaných měření vědcům zjistit, nakolik jsou si jisti průměrným číslem. Při rozhodování, zda měření z experimentu souhlasí s předpovědí, je směrodatná odchylka těchto měření velmi důležitá. Pokud je průměrné číslo z experimentů příliš vzdálené od předpovězeného čísla (přičemž vzdálenost se měří ve směrodatných odchylkách), pak testovaná teorie nemusí být správná. Viz interval předpovědi.
Příklady použití
Směrodatná odchylka souboru hodnot je užitečná pro poznání, jak velký rozdíl od "průměru" (střední hodnoty) lze očekávat.
Počasí
Jako jednoduchý příklad uveďme průměrné denní teploty dvou měst, jednoho ve vnitrozemí a druhého v blízkosti oceánu. Je užitečné si uvědomit, že rozsah denních vysokých teplot pro města v blízkosti oceánu je menší než pro města ve vnitrozemí. Každé z těchto dvou měst může mít stejnou průměrnou denní teplotu. Směrodatná odchylka denní vysoké teploty pro pobřežní město však bude menší než pro město ve vnitrozemí .
Sport
Dalším způsobem, jak se na to dívat, je vzít v úvahu sportovní týmy. V každém sportu existují týmy, které jsou v něčem dobré a v něčem ne. Týmy, které se umístí nejvýše, nebudou vykazovat velké rozdíly ve schopnostech. Daří se jim ve většině kategorií. Čím nižší je směrodatná odchylka jejich schopností v jednotlivých kategoriích, tím vyrovnanější a konzistentnější jsou. Týmy s vyšší směrodatnou odchylkou však budou méně předvídatelné. Tým, který je obvykle špatný ve většině kategorií, bude mít nízkou směrodatnou odchylku. Tým, který je obvykle dobrý ve většině kategorií, bude mít také nízkou směrodatnou odchylku. Tým s vysokou směrodatnou odchylkou však může být typem týmu, který získává mnoho bodů (silný útok), ale zároveň umožňuje druhému týmu získat mnoho bodů (slabá obrana).
Snaha zjistit dopředu, které týmy vyhrají, může zahrnovat sledování směrodatných odchylek různých týmových "statistik". Čísla, která se liší od očekávaných, mohou porovnat silné a slabé stránky a ukázat, jaké důvody mohou být nejdůležitější pro poznání, který tým vyhraje.
Při závodění se měří čas, za který jezdec ujede každé kolo na trati. Jezdec s nízkou směrodatnou odchylkou času na kolo je konzistentnější než jezdec s vyšší směrodatnou odchylkou. Tyto informace lze využít k pochopení toho, jak může jezdec zkrátit čas potřebný k dokončení kola.
Peníze
V penězích může směrodatná odchylka znamenat riziko, že cena vzroste nebo klesne (akcie, dluhopisy, nemovitosti atd.). Může také znamenat riziko, že skupina cen půjde nahoru nebo dolů (aktivně spravované podílové fondy, indexové podílové fondy nebo ETF). Riziko je jedním z důvodů, proč se rozhodovat o tom, co koupit. Riziko je číslo, podle kterého lidé mohou zjistit, kolik peněz mohou vydělat nebo ztratit. S rostoucím rizikem může být výnos z investice vyšší, než se očekává ("plusová" směrodatná odchylka). Investice však může také ztratit více peněz, než se očekávalo (směrodatná odchylka "minus").
Například si člověk musel vybrat mezi dvěma akciemi. Akcie A měla za posledních 20 let průměrný výnos 10 % se směrodatnou odchylkou 20 procentních bodů (p.b.). Akcie B měla za posledních 20 let průměrný výnos 12 %, ale vyšší směrodatnou odchylku 30 p.b.. Po zvážení rizika se osoba může rozhodnout, že akcie A je bezpečnější volbou. I když možná nevydělá tolik peněz, pravděpodobně ani mnoho peněz neztratí. Osoba si může myslet, že akcie B s průměrem vyšším o 2 procentní body nestojí za dodatečnou standardní odchylku 10 p.b. (větší riziko nebo nejistotu očekávaného výnosu).
Pravidla pro normálně rozdělená čísla
Většina matematických rovnic pro směrodatnou odchylku předpokládá, že čísla jsou rozdělena normálně. To znamená, že čísla jsou rozložena určitým způsobem na obou stranách průměrné hodnoty. Normální rozdělení se také nazývá Gaussovo rozdělení, protože ho objevil Carl Friedrich Gauss. Často se mu říká zvonová křivka, protože čísla se rozloží tak, že na grafu vytvoří tvar zvonu.
Čísla nejsou normálně rozdělena, pokud jsou seskupena na jedné nebo druhé straně průměrné hodnoty. Čísla mohou být rozložena a přesto jsou normálně rozdělena. Směrodatná odchylka vypovídá o tom, jak moc jsou čísla rozložena.

Tmavě modrá je méně než jedna směrodatná odchylka od průměru. U normálního rozdělení zahrnuje 68,27 % čísel, zatímco dvě směrodatné odchylky od průměru (střední a tmavě modrá) zahrnují 95,45 %, tři směrodatné odchylky (světle, středně a tmavě modrá) zahrnují 99,73 % a čtyři směrodatné odchylky představují 99,994 %.
Vztah mezi průměrem (průměrem) a směrodatnou odchylkou
Průměr (průměr) a směrodatná odchylka souboru dat se obvykle zapisují společně. Člověk pak může pochopit, jaké je průměrné číslo a jak široce jsou ostatní čísla ve skupině rozložena.
Rozložení skupiny čísel lze také vyjádřit pomocí variačního koeficientu, což je směrodatná odchylka dělená průměrem. Je to bezrozměrné číslo. Variační koeficient se často násobí 100 % a zapisuje se v procentech.
Historie
Termín směrodatná odchylka poprvé písemně použil Karl Pearson v roce 1894 poté, co jej použil na přednáškách. Bylo to jako náhrada dřívějších názvů pro stejnou myšlenku: například Gauss používal střední chybu.
Související stránky
- Přesnost a preciznost
- Velikost vzorku
Otázky a odpovědi
Otázka: Co je to směrodatná odchylka?
Odpověď: Směrodatná odchylka je číslo, které se používá k určení toho, jak jsou naměřené hodnoty skupiny rozptýleny od průměru (střední nebo očekávané hodnoty).
Otázka: Co znamená nízká směrodatná odchylka?
Odpověď: Nízká směrodatná odchylka znamená, že většina čísel se blíží průměru.
Otázka: Co znamená vysoká směrodatná odchylka?
Odpověď: Vysoká směrodatná odchylka znamená, že čísla jsou více rozptýlena.
Otázka: Jak se standardní odchylka používá v penězích?
Odpověď: V penězích ukazuje směrodatná odchylka dosaženého úroku, jak moc se může lišit dosažený úrok jedné osoby od průměru.
Otázka: Kdy lze měřit pouze část skupiny?
Odpověď: Mnohokrát lze měřit pouze vzorek nebo část skupiny.
Otázka: Jak je znázorněna směrodatná odchylka celé skupiny?
Odpověď: Směrodatná odchylka celé skupiny je reprezentována řeckým písmenem َ {\displaystyle \sigma }. .
Otázka: Jak je znázorněna směrodatná odchylka vzorku?
Odpověď: Směrodatná odchylka vzorku je reprezentována písmenem s {\displaystyle s} .
Vyhledávání



