Fourierova transformace
Fourierova transformace je matematická funkce, kterou lze použít k nalezení základních frekvencí, z nichž se skládá signál nebo vlna. Například při přehrávání akordu lze zvukovou vlnu akordu vložit do Fourierovy transformace a zjistit, z jakých tónů se akord skládá. Výstup Fourierovy transformace se někdy nazývá frekvenční spektrum nebo rozdělení, protože zobrazuje spektrum frekvencí vstupu. Tato funkce má mnohostranné využití v kryptografii, oceánografii, strojovém učení, radiologii, kvantové fyzice a také při návrhu a vizualizaci zvuku.
Fourierova transformace funkce f ( x ) {\displayystyle f(x)}
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx}
α {\displaystyle \alpha } 
F ( α ) {\displaystyle F(\alpha )}

e - 2 π i α x {\displaystyle e^{-2\pi i\alfa x}} 

Inverzní Fourierova transformace je dána vztahem
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alfa )e^{+2\pi ix\alfa }d\alfa }
Fourierova transformace ukazuje, jaké frekvence se v signálu nacházejí. Uvažujme například zvukovou vlnu, která obsahuje tři různé hudební tóny: Zhotovení grafu Fourierovy transformace této zvukové vlny (s frekvencí na ose x a intenzitou na ose y) ukáže vrchol na každé frekvenci, který odpovídá jedné z hudebních not.
Sčítáním kosinusů a sinusů s různými amplitudami a frekvencemi lze vytvořit mnoho signálů. Fourierova transformace zobrazuje amplitudy a fáze těchto kosinusů a sinusů v závislosti na jejich frekvencích.
Fourierova transformace je důležitá, protože mnoho signálů dává větší smysl, když jsou jejich frekvence odděleny. Ve výše uvedeném příkladu se zvukem není při pohledu na signál vzhledem k času zřejmé, že v signálu jsou tóny A, B a C. Mnoho systémů dělá různé věci s různými frekvencemi, takže tyto druhy systémů lze popsat podle toho, co dělají s jednotlivými frekvencemi. Příkladem je filtr, který blokuje vysoké frekvence.
Výpočet Fourierovy transformace vyžaduje znalost integrace a imaginárních čísel. K výpočtu Fourierovy transformace se kromě nejjednodušších signálů obvykle používají počítače. Rychlá Fourierova transformace je metoda, kterou počítače používají k rychlému výpočtu Fourierovy transformace.
· 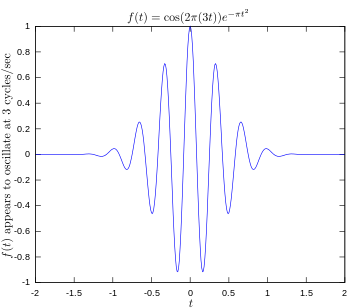
Původní funkce zobrazující signál kmitající rychlostí 3 hertze.
· 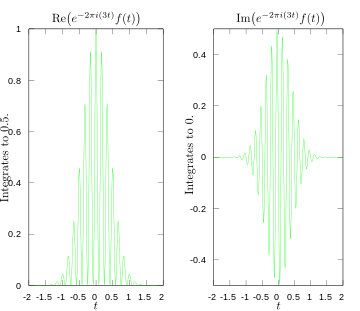
Reálná a imaginární část integrálu pro Fourierovu transformaci při frekvenci 3 Hz
· 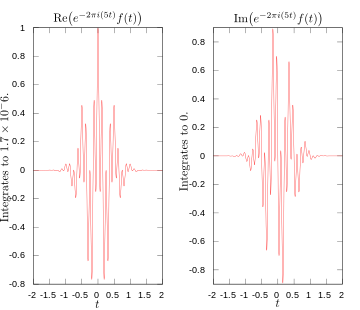
Reálná a imaginární část integrálu pro Fourierovu transformaci při frekvenci 5 hertzů
· 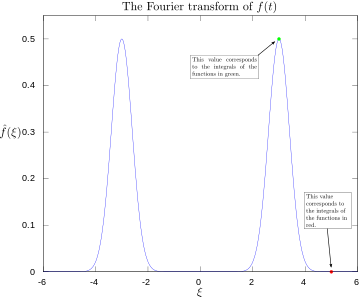
Fourierova transformace s označením 3 a 5 hertzů.
Otázky a odpovědi
Otázka: Co je to Fourierova transformace?
Odpověď: Fourierova transformace je matematická funkce, kterou lze použít ke zjištění základních frekvencí, z nichž se skládá vlna. Vezme komplexní vlnu a najde frekvence, které ji tvoří, což umožňuje určit tóny, které tvoří akord.
Otázka: Jaká jsou některá využití Fourierovy transformace?
Odpověď: Fourierova transformace má mnoho využití v kryptografii, oceánografii, strojovém učení, radiologii, kvantové fyzice a také v designu a vizualizaci zvuku.
Otázka: Jak se Fourierova transformace počítá?
Odpověď: Fourierova transformace funkce f(x) je dána vztahem F(ב) = ∫-∞+∞f(x)e-2נiבxdx, kde ב je frekvence. Vrátí se hodnota vyjadřující, jak převažující je frekvence ב v původním signálu. Inverzní Fourierova transformace je dána vztahem f(x) = ∫-∞+∞F(ב)e+2נixבdב.
Otázka: Jak vypadá výstup Fourierovy transformace?
Odpověď: Výstup Fourierovy transformace lze nazvat buď frekvenčním spektrem, nebo rozdělením, protože zobrazuje rozdělení možných frekvencí vstupu.
Otázka: Jak počítače počítají rychlou Fourierovu transformaci?
Odpověď: Počítače používají algoritmus zvaný rychlá Fourierova transformace (FFT), který umožňuje rychlý výpočet transformací jakýchkoli signálů, kromě těch nejjednodušších.
Otázka: Co nám neukazuje pohled na signály vzhledem k času?
Odpověď: Při pohledu na signály vzhledem k času není zřejmé, jaké tóny se v nich vyskytují; mnoho signálů dává větší smysl, když se jejich frekvence oddělí a analyzují jednotlivě.
Vyhledávání

