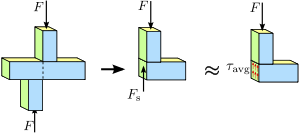Mechanické napětí
Napětí je síla na jednotku plochy působící na těleso, která má tendenci způsobit změnu jeho tvaru.
Napětí je mírou vnitřních sil mezi částicemi tělesa. Tyto vnitřní síly jsou reakcí na vnější síly působící na těleso, které způsobují jeho oddělení, stlačení nebo sesunutí. Vnější síly jsou buď povrchové síly, nebo síly tělesa. Napětí je průměrná síla na jednotku plochy, kterou částice tělesa působí na sousední částici přes pomyslnou plochu, která je odděluje.
Vzorec pro jednoosé normálové napětí je:
σ = F A {\displaystyle {\sigma }={\frac {F}{A}}})
kde σ je napětí, F je síla a A je plocha.
V jednotkách SI se síla měří v newtonech a plocha v metrech čtverečních. To znamená, že napětí je v newtonech na metr čtvereční neboli N/m2. Napětí má však vlastní jednotku SI, která se nazývá pascal. 1 pascal (symbol Pa) se rovná 1 N/m2. V imperiálních jednotkách se napětí měří v librách síly na čtvereční palec, což se často zkracuje na "psi". Rozměr napětí je stejný jako rozměr tlaku.
V mechanice kontinua se zatížené deformovatelné těleso chová jako kontinuum. Tyto vnitřní síly jsou tedy v objemu hmotného tělesa rozloženy spojitě. (To znamená, že rozložení napětí v tělese je vyjádřeno jako po částech spojitá funkce prostoru a času.) Síly způsobují deformaci tvaru tělesa. Deformace může vést k trvalé změně tvaru nebo k porušení konstrukce, pokud materiál není dostatečně pevný.
Některé modely mechaniky kontinua považují sílu za něco, co se může měnit. Jiné modely se zabývají deformací hmoty a pevných těles, protože vlastnosti hmoty a pevných těles jsou trojrozměrné. Každý z těchto přístupů může dávat různé výsledky. Klasické modely mechaniky kontinua předpokládají průměrnou sílu a nezahrnují správně "geometrické faktory". (Geometrie tělesa může být důležitá pro to, jak se rozděluje napětí a jak se hromadí energie při působení vnější síly.)
Obrázek 1.4 Smykové napětí v prizmatické tyči. Rozložení napětí nebo síly v průřezu tyče nemusí být nutně rovnoměrné. Nicméně průměrné smykové napětí τ a v g {\displaystyle \tau _{\mathrm {avg} }\,\! }
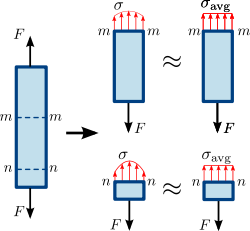
Obrázek 1.3 Normálové napětí v prizmatické tyči (přímý prut s rovnoměrným průřezem). Rozložení napětí nebo síly v průřezu tyče nemusí být nutně rovnoměrné. Nicméně průměrné normálové napětí σ a v g {\displaystyle \sigma _{\mathrm {avg} }\,\! }
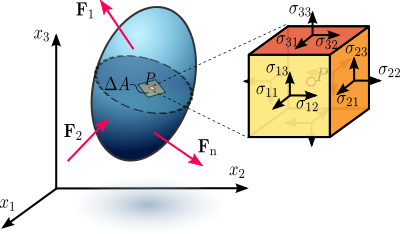
Obrázek 1.1 Napětí v zatíženém deformovatelném hmotném tělese, které se předpokládá jako kontinuum.
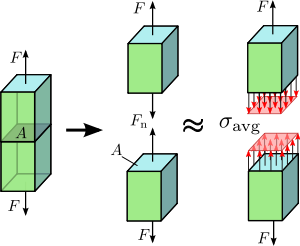
Obrázek 1.2 Axiální napětí v osově zatížené prizmatické tyči.
Smykové napětí
Další informace: Smykové napětí
Jednoduché napětí
V některých situacích lze napětí v objektu popsat jediným číslem nebo jediným vektorem (číslo a směr). Tři takové jednoduché napěťové situace jsou jednoosé normálové napětí, jednoduché smykové napětí a izotropní normálové napětí.
Jednoosé normálové napětí
Napětí v tahu (nebo tahu) je stav napětí, který vede k roztažnosti; to znamená, že délka materiálu má tendenci se zvětšovat ve směru tahu. Objem materiálu zůstává konstantní. Působí-li na těleso stejné a opačné síly, pak se napětí způsobené touto silou nazývá tahové napětí.
Proto se v jednoosém materiálu délka zvětšuje ve směru tahového napětí a v ostatních dvou směrech se zmenšuje. Při jednoosém způsobu tahu je tahové napětí vyvoláno tahovými silami. Tahové napětí je opakem napětí v tlaku.
Konstrukčními prvky v přímém tahu jsou lana, zemní kotvy a hřebíky, šrouby atd. Nosníky namáhané ohybovými momenty mohou zahrnovat napětí v tahu i v tlaku a/nebo ve smyku.
Napětí v tahu lze zvyšovat až do dosažení pevnosti v tahu, tj. mezního stavu napětí.
Napětí v jednorozměrných tělesech
Všechny reálné objekty zaujímají trojrozměrný prostor. Pokud jsou však dva rozměry v porovnání s ostatními velmi velké nebo velmi malé, může být objekt modelován jako jednorozměrný. To zjednodušuje matematické modelování objektu. Mezi jednorozměrné objekty patří kus drátu zatížený na koncích a viděný z boku a plech zatížený na čelní straně a viděný zblízka a v průřezu.
Související stránky
- Napětí
- Ohýbání
Otázky a odpovědi
Otázka: Co je to stres?
Odpověď: Napětí je síla na jednotku plochy působící na těleso, která má tendenci způsobit změnu jeho tvaru. Je to míra vnitřních sil v tělese mezi jeho částicemi a je to průměrná síla na jednotku plochy, kterou částice tělesa působí na sousední částici přes pomyslnou plochu, která je odděluje.
Otázka: Jak ovlivňují vnější síly napětí?
Odpověď: Vnější síly jsou buď povrchové síly, nebo síly působící na těleso a způsobují deformaci tvaru tělesa, která může vést k trvalé změně tvaru nebo k porušení konstrukce, pokud materiál není dostatečně pevný.
Otázka: Jaký je vzorec pro jednoosé normálové napětí?
Odpověď: Vzorec pro jednoosé normálové napětí je σ = F/A, kde σ je napětí, F je síla a A je plocha. V jednotkách SI se síla měří v newtonech a plocha v metrech čtverečních, což znamená, že napětí je newton na metr čtvereční (N/m2). Pro napětí však existuje vlastní jednotka SI zvaná pascal (Pa), která se rovná 1 N/m2. V imperiálních jednotkách by se měřilo v librách síly na čtvereční palec (psi).
Otázka: Co předpokládá mechanika kontinua o síle?
Odpověď: Klasické modely mechaniky kontinua předpokládají průměrnou sílu a nezahrnují správně geometrické faktory - to znamená, že neberou v úvahu, jak geometrie ovlivňuje to, jak se při působení vnější síly hromadí energie.
Otázka: Jak mohou různé modely poskytovat různé výsledky při pohledu na deformaci hmoty a pevných těles?
Odpověď: Různé modely se na deformaci hmoty a pevných těles dívají různě, protože vlastnosti hmoty a pevných těles jsou trojrozměrné - každý přístup tedy bere v úvahu jiné aspekty, což může vést k různým výsledkům.
Otázka: Jak mechanika kontinua přistupuje k zatíženým deformovatelným tělesům?
Odpověď: Mechanika kontinua přistupuje k zatíženým deformovatelným tělesům jako ke kontinuím - to znamená, že vnitřní síly jsou rozloženy plynule v objemu hmotného tělesa, místo aby byly soustředěny v určitých bodech jako u klasických modelů.
Vyhledávání