Pravděpodobnostní prostor
Pravděpodobnostní prostor je matematický model používaný k popisu vědeckých experimentů Pravděpodobnostní prostor se skládá ze tří částí:
- Vzorkovací prostor, který obsahuje všechny možné výsledky
- Soubor událostí. Ke každé události se váže nula nebo více výsledků
- Funkce, která přiřazuje pravděpodobnosti jednotlivým událostem.
Výsledek je výsledkem jednoho provedení modelu. Vzhledem k tomu, že jednotlivé výsledky mohou mít malý praktický význam, používají se složitější události k charakterizaci skupin výsledků. Soubor všech takových událostí je σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}). 
. Nakonec je třeba určit pravděpodobnost výskytu každé události. To se provádí pomocí funkce míry pravděpodobnosti P.
Jakmile je vytvořen prostor pravděpodobnosti, předpokládá se, že "příroda" provede svůj tah a vybere jeden výsledek, ω, z výběrového prostoru Ω. O všech událostech v F {\displaystyle \scriptstyle {\mathcal {F}}}, které obsahují vybraný výsledek ω (připomeňme, že každá událost je podmnožinou Ω), se říká, že "nastaly". Výběr prováděný přírodou probíhá tak, že kdyby se experiment opakoval nekonečně mnohokrát, relativní četnosti výskytu jednotlivých událostí by se shodovaly s pravděpodobnostmi předepsanými funkcí P.
Významný sovětský matematik Andrej Kolmogorov zavedl pojem pravděpodobnostního prostoru spolu s dalšími axiomy pravděpodobnosti ve 30. letech 20. století.
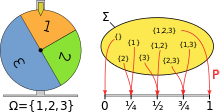
Modelování kola štěstí pomocí pravděpodobnostního prostoru
Otázky a odpovědi
Otázka: Co je to pravděpodobnostní prostor?
Odpověď: Pravděpodobnostní prostor je matematický model používaný k popisu vědeckých experimentů. Skládá se ze tří částí: výběrového prostoru, který obsahuje seznam všech možných výsledků, množiny událostí, které spojují nula nebo více výsledků, a funkce, která každé události přiřazuje pravděpodobnost.
Otázka: Z čeho se skládá výběrový prostor?
Odpověď: Výběrový prostor se skládá ze všech možných výsledků, často zapisovaných jako Ω {\displaystyle \Omega }. a výsledek jako ω {\displaystyle \Omega }. .
Otázka: Co je to výsledek?
Odpověď: Výsledek je výsledek jednoho provedení modelu.
Otázka: K čemu se v pravděpodobnostních prostorech používají události?
Odpověď: Události se používají k charakterizaci skupin výsledků, protože jednotlivé výsledky mohou mít jen malý praktický význam. Soubor všech takových událostí se nazývá σ-algebra, někdy se zapisuje jako F {\displaystyle {\mathcal {F}}} .
Otázka: Jak se přiřazují pravděpodobnosti jednotlivým událostem?
Odpověď: Pravděpodobnosti se každé události přiřazují pomocí funkce míry pravděpodobnosti P.
Otázka: Kdo zavedl pojem pravděpodobnostních prostorů? Odpověď: Významný sovětský matematik Andrej Kolmogorov zavedl pojem pravděpodobnostních prostorů spolu s dalšími axiomy pravděpodobnosti ve 30. letech 20. století.
