Zlatý řez
Když máme jedno číslo a a druhé menší číslo b, zjistíme jejich poměr tak, že je vydělíme. Jejich poměr je a/b. Další poměr zjistíme tak, že obě čísla sečteme a+b a vydělíme větším číslem a. Nový poměr je (a+b)/a. Pokud se tyto dva poměry rovnají stejnému číslu, pak se toto číslo nazývá zlatý řez. Řecké písmeno φ {\displaystyle \varphi } 
(fí) se obvykle používá jako název pro zlatý řez.
Například pokud b = 1 a a/b = φ {\displaystyle \varphi } , pak a = φ {\displaystyle \varphi } . Druhý poměr (a+b)/a je pak ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi }. 
. Protože se tyto dva poměry rovnají, je to pravda:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}
Jedním ze způsobů, jak toto číslo zapsat, je
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}}
5 {\displaystyle {\sqrt {5}}}
je jako každé číslo, které po vynásobení sebou samým tvoří 5 (nebo které číslo se násobí): 5 × 5 = 5 {\displaystyle {\sqrt {5}}}krát {\sqrt {5}}=5}}
.
Zlatý řez je iracionální číslo. Pokud se ho člověk pokusí zapsat, nikdy se nezastaví a nikdy nevytvoří vzorec, ale začne takto: 1,6180339887... Důležitou věcí u tohoto čísla je, že člověk od něj může odečíst 1 nebo jím 1 vydělit. Ať tak či onak, číslo bude stále pokračovat a nikdy se nezastaví.
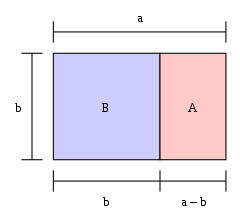
Zlatý obdélník
Pokud se délka obdélníku dělená jeho šířkou rovná zlatému řezu, jedná se o "zlatý obdélník". Pokud z jednoho konce zlatého obdélníku odřízneme čtverec, pak druhý konec je nový zlatý obdélník. Na obrázku je velký obdélník (modrý a růžový dohromady) zlatý obdélník, protože a / b = φ {\displayystyle a/b=\varphi }. 
. Modrá část (B) je čtverec. Růžová část sama o sobě (A) je další zlatý obdélník, protože b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi }. 
. Velký obdélník a růžový obdélník mají stejný tvar, ale růžový obdélník je menší a je otočený.
Velký obdélník BA je zlatý obdélník; to znamená, že poměr b:a je 1: φ {\displaystyle \varphi } . Pro každý takový obdélník, a to pouze pro obdélníky s tímto konkrétním poměrem, platí, že pokud odstraníme čtverec B, zůstane A jako další zlatý obdélník, tj. se stejným poměrem jako původní obdélník.
Fibonacciho čísla
Fibonacciho čísla jsou seznamem čísel. Další číslo v seznamu lze najít sečtením posledních dvou čísel. Pokud člověk vydělí číslo v seznamu číslem, které mu předcházelo, tento poměr se stále více blíží zlatému řezu.
| Fibonacciho číslo | děleno předcházejícím | poměr |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Zlatý řez v přírodě
V přírodě se zlatý řez často používá pro uspořádání listů nebo květů. Ty využívají zlatý úhel přibližně 137,5 stupně. Listy nebo květy uspořádané v tomto úhlu nejlépe využívají sluneční světlo.
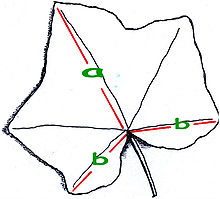
List břečťanu obecného znázorňující zlatý řez
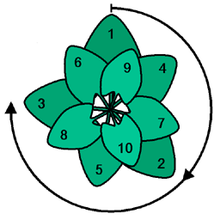
Použití zlatého úhlu optimálně využije sluneční světlo. Toto je pohled shora.
Otázky a odpovědi
Otázka: Jaký je poměr dvou čísel?
Odpověď: Poměr dvou čísel zjistíme tak, že je vydělíme, takže poměr bude a/b.
Otázka: Jak lze zjistit jiný poměr?
Odpověď: Další poměr lze zjistit tak, že obě čísla sečteme a tento součet vydělíme větším číslem a. Tento nový poměr by byl (a+b)/a.
Otázka: Jak se nazývá situace, kdy se tyto dva poměry navzájem rovnají?
Odpověď: Když se tyto dva poměry navzájem rovnají, nazývá se zlatý řez. Obvykle se označuje řeckým písmenem צ nebo phi.
Otázka: Jestliže b = 1 a a/b = צ , co to znamená pro a?
Odpověď: Je-li b = 1 a a/b = צ , pak to znamená, že a = צ.
Otázka: Jak lze toto číslo zapsat?
Odpověď: Jedním ze způsobů, jak toto číslo zapsat, je צ = 1 + 5 / 2 = 1,618...
Otázka: Co znamená, když od něj odečteme 1 nebo jím vydělíme 1?
Odpověď: Pokud od něj odečtete 1 nebo jím 1 vydělíte, dostanete zpět stejné číslo - jinými slovy, obě se budou rovnat zlatému řezu.
Otázka: Je zlatý řez iracionální číslo?
Odpověď: Ano, zlatý poměr je iracionální číslo, což znamená, že pokud se ho někdo pokusí vypsat, nikdy nebude mít konec a žádný vzor - pouze začíná něčím jako "1,6180339887...".
