Válec
Válec je jeden z nejzákladnějších zakřivených geometrických útvarů, jehož povrch tvoří body v pevné vzdálenosti od dané úsečky, známé jako osa válce. Tento tvar si lze představit jako kruhový hranol. Jak povrch, tak uvnitř vytvořený pevný tvar lze nazvat válcem. Povrch a objem válce jsou známy již od starověku.
V diferenciální geometrii je válec definován šířeji jako jakákoli vládnoucí plocha, která je protnuta jednoparametrovou rodinou rovnoběžných přímek. Válec, jehož průřez je elipsa, parabola nebo hyperbola, se nazývá eliptický válec, parabolický válec, resp. hyperbolický válec.
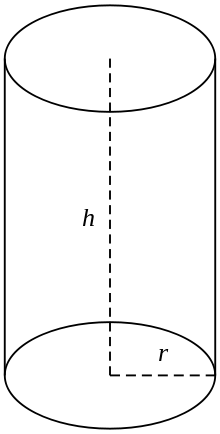
Pravý kruhový válec
Běžné použití
V běžném použití se válcem rozumí konečný řez pravým kruhovým válcem, tj. válcem s generujícími přímkami kolmými k základnám, jehož konce jsou uzavřeny tak, že tvoří dvě kruhové plochy, jako na obrázku (vpravo). Má-li válec poloměr r a délku (výšku) h, pak je jeho objem dán vztahem:
V = πrh2
a jeho povrch je:
- plocha vrcholu (πr2) +
- plocha dna (πr2) +
- plocha strany (2πrh).
Bez horní a dolní části (boční plochy) je tedy plocha:
A = 2πrh.
S horní a spodní částí je plocha:
A = 2πr2 + 2πrh = 2πr(r + h).
Pro daný objem má válec s nejmenším povrchem h = 2r. Pro daný povrch má válec s největším objemem h = 2r, tj. válec se vejde do krychle (výška = průměr).
Svazek
Pravoúhlý válec o výšce h jednotek a podstavě o poloměru r jednotek se souřadnicovými osami zvolenými tak, že počátek je ve středu jedné podstavy a výška se měří podél kladné osy x. Rovinný řez ve vzdálenosti x jednotek od počátku má plochu A(x) čtverečních jednotek, kde
A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}}
nebo
A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}}
Prvek objemu je pravý válec o podstavě Awi čtverečních jednotek a tloušťce Δxi jednotek. Je-li tedy V krychlových jednotek objem pravého kruhového válce, podle Riemannových součtů,
V o l u m e c y l i n d e r = lim | | Δ → |0 | ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {Objem\;z\;válec} =\lim _{|\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x}
= ∫0 h A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}
= ∫ 0h π r d2 y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Pomocí válcových souřadnic lze objem vypočítat integrací přes
= ∫ 0h0 ∫ 2π ∫ 0r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s,\,ds\,d\phi \,dz}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Válcový průřez
Válcové řezy jsou průsečíky válců s rovinami. Pro pravý kruhový válec existují čtyři možnosti. Rovina, která je k válci tečná, se s válcem setkává v jedné přímce. Pohybuje-li se rovina rovnoběžně sama se sebou, buď válec neprotíná, nebo jej protíná ve dvou rovnoběžných přímkách. Všechny ostatní roviny protínají válec v elipse nebo, jsou-li kolmé na osu válce, v kružnici.
Ostatní typy válců
Eliptický válec neboli cylindroid je kvadrická plocha s následující rovnicí v kartézských souřadnicích:
( x a ) + 2( y b ) =21 . {\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=1.}
Tato rovnice platí pro eliptický válec, který je zobecněním běžného kruhového válce (a = b). Ještě obecnější je zobecněný válec: průřezem může být libovolná křivka.
Válec je degenerovaný kvadrik, protože alespoň jedna ze souřadnic (v tomto případě z) se v rovnici nevyskytuje.
Šikmý válec má horní a dolní plochu vzájemně posunutou.
Existují i další neobvyklé typy válců. Jedná se o pomyslné eliptické válce:
( x a ) + 2( y b ) =2 - 1{\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1}
hyperbolický válec:
( x a )2 - ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1}}
a parabolického válce:
x +2 a 2y =0 . {\displaystyle x^{2}+2ay=0.\,}

Eliptický válec

V projektivní geometrii je válec jednoduše kužel, jehož vrchol je v nekonečnu, což vizuálně odpovídá tomu, že válec v perspektivě vypadá jako kužel směrem k obloze.
Projektivní geometrie
V projektivní geometrii je válec jednoduše kužel, jehož vrchol je v nekonečnu.
To je užitečné při definování degenerovaných kuželoseček, které vyžadují uvažování válcových kuželoseček.
Otázky a odpovědi
Otázka: Co je to válec?
Odpověď: Válec je trojrozměrný geometrický útvar, jehož povrch tvoří body v pevné vzdálenosti od dané úsečky, známé jako osa válce. Lze si jej představit jako kruhový hranol a povrch i těleso vytvořené uvnitř lze nazvat válcem.
Otázka: Jak dlouho už lidé znají povrch a objem válců?
Odpověď: Povrch a objem válců jsou známy již od starověku.
Otázka: Co jsou to eliptické, parabolické a hyperbolické válce?
Odpověď: Eliptické, parabolické a hyperbolické válce jsou válce, jejichž průřez je elipsa, parabola, resp. hyperbola.
Otázka: Jak je válec definován v diferenciální geometrii?
Odpověď: V diferenciální geometrii je válec definován šířeji jako vládnoucí plocha, která je protnuta jednoparametrovou rodinou rovnoběžných přímek.
Otázka: Co znamená, že je něco "ovládáno"?
Odpověď: "Vládnout" znamená, že je na něm nějakým způsobem nakreslena přímka.
Otázka: Existuje pouze jeden typ válce?
Odpověď: Ne, existuje mnoho různých typů válců, například eliptické, parabolické a hyperbolické válce, které mají různé průřezy.
Vyhledávání










