Magnetický moment

Dvě definice momentu

V učebnicích se k definici magnetických momentů používají dva vzájemně se doplňující přístupy. V učebnicích z doby před rokem 1930 byly definovány pomocí magnetických pólů. Většina novějších učebnic je definuje pomocí Ampérových proudů.

Definice magnetického pólu

Fyzikové představují zdroje magnetických momentů v materiálech jako póly. Severní a jižní pól jsou analogií kladného a záporného náboje v elektrostatice. Uvažujme tyčový magnet, který má magnetické póly stejné velikosti, ale opačné polarity. Každý pól je zdrojem magnetické síly, která se vzdáleností slábne. Protože magnetické póly jsou vždy v páru, jejich síly se částečně ruší, protože zatímco jeden pól přitahuje, druhý odpuzuje. Toto rušení je největší, když jsou póly blízko sebe, tj. když je tyčový magnet krátký. Magnetická síla, kterou tyčový magnet v daném bodě prostoru vytváří, tedy závisí na dvou faktorech: jednak na síle p {\displaystyle p} jeho pólů, jednak na vektoru l {\displaystyle \mathbf {l}. }, které je oddělují. Moment je definován jako

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . }

Ukazuje ve směru od jižního k severnímu pólu. Analogii s elektrickými dipóly bychom neměli brát příliš vážně, protože magnetické dipóly jsou spojeny s momentem hybnosti (viz Magnetický moment a moment hybnosti). Přesto jsou magnetické póly velmi užitečné pro magnetostatické výpočty, zejména v aplikacích pro feromagnety. Praktici používající přístup magnetických pólů obvykle reprezentují magnetické pole irotačním polem H {\displaystyle \mathbf {H}. } v analogii s elektrickým polem E {\displaystyle \mathbf {E}. } .

Definice proudové smyčky

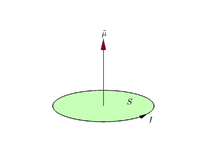
Předpokládejme, že rovinná uzavřená smyčka přenáší elektrický proud I {\displaystyle I} a má vektorovou plochu S {\displaystyle \mathbf {S}. } ( x {\displaystyle x} , y {\displaystyle y} Souřadnice z {\displaystyle z} tohoto vektoru jsou plochy projekcí smyčky na y z {\displaystyle yz}. , z x {\displaystyle zx}. a x y {\displaystyle xy} roviny). Její magnetický moment m {\displaystyle \mathbf {m} } , vektor, je definován jako:

m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . }

Směr vektorové plochy je podle konvence dán pravidlem úchopu pravé ruky (stočení prstů pravé ruky ve směru proudu kolem smyčky, kdy se dlaň "dotýká" vnějšího okraje smyčky, a rovný palec ukazuje směr vektorové plochy, a tedy magnetického momentu).

Pokud smyčka není rovinná, je moment dán jako

m = I 2∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . }

V nejobecnějším případě libovolného rozložení proudu v prostoru lze magnetický moment takového rozložení zjistit z následující rovnice:

m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,}

kde r {\displaystyle \mathbf {r} } je polohový vektor směřující z počátku do místa prvku objemu a J {\displaystyle \mathbf {J} je polohový vektor směřující z počátku do místa prvku objemu a J {\displaystyle \mathbf {J} je polohový vektor směřující z počátku do místa prvku objemu. } je vektor proudové hustoty v tomto místě.

Výše uvedenou rovnici lze použít pro výpočet magnetického momentu libovolné sestavy pohybujících se nábojů, například rotujícího nabitého tělesa, a to tak, že nahradíme

J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,}

kde ρ {\displaystyle \rho } je hustota elektrického náboje v daném bodě a v {\displaystyle \mathbf {v} } je okamžitá lineární rychlost tohoto bodu.

Například magnetický moment elektrického náboje, který se pohybuje po kruhové dráze, je následující

m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} } ,

kde r {\displaystyle \mathbf {r} } je poloha náboje q {\displaystyle q} vzhledem ke středu kružnice a v {\displaystyle \mathbf {v} } je okamžitá rychlost náboje.

Praktici používající model proudové smyčky obvykle reprezentují magnetické pole solenoidovým polem B {\displaystyle \mathbf {B}. } analogicky elektrostatickému poli D {\displaystyle \mathbf {D}). } .

Magnetický moment solenoidu

Zobecněním výše uvedené proudové smyčky je víceotáčková cívka neboli solenoid. Její moment je vektorovým součtem momentů jednotlivých závitů. Má-li solenoid N {\displayystyle N} stejných závitů (jednovrstvé vinutí),

m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . }

Trojrozměrný obraz solenoidu.


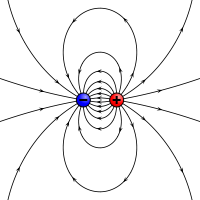
Elektrostatická obdoba magnetického momentu: dva protilehlé náboje oddělené konečnou vzdáleností.

Jednotky

Jednotka magnetického momentu není základní jednotkou v Mezinárodní soustavě jednotek (SI) a lze ji znázornit více způsoby. Například v definici proudové smyčky se plocha měří v metrech čtverečních a I {\displaystyle I} se měří v ampérech, takže magnetický moment se měří v ampérech čtverečních ( A m {\displaystyle2 {\text{A m}}^{2}} ). V rovnici pro moment na momentu se moment měří v newtonmetrech a magnetické pole v teslech, takže moment se měří v N.m na tesla ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}} ). Tyto dvě reprezentace jsou ekvivalentní:

A m = 2N.m T - 1. {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. }

V systému CGS existuje několik různých sad elektromagnetických jednotek, z nichž hlavní jsou ESU, Gaussian a EMU. Mezi nimi existují v systému CGS dvě alternativní (neekvivalentní) jednotky magnetického dipólového momentu:

(ESU CGS) 1 statA-cm² = 3,33564095×10^-14 (m-A² nebo N.m/T)

a (častěji používané)

(EMU CGS a Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10^-3 (m-A² nebo N.m/T).

Poměr těchto dvou neekvivalentních jednotek CGS (EMU/ESU) se přesně rovná rychlosti světla ve volném prostoru vyjádřené v cm/s.

Všechny vzorce v tomto článku jsou správné v jednotkách SI, ale v jiných soustavách jednotek může být nutné vzorce změnit. Například v jednotkách SI má proudová smyčka s proudem I a plochou A magnetický moment I×A (viz níže), ale v Gaussových jednotkách je magnetický moment I×A/c.

Vlastní magnetické momenty a spiny některých elementárních částic
Částice	Magnetický dipólový moment v jednotkách SI (10 −27J/T)	Spinové kvantové číslo (bezrozměrné)
elektrony	-9284.764	1/2
proton	14.106067	1/2
neutronové	-9.66236	1/2
mion	-44.904478	1/2
deuteron	4.3307346	1
triton	15.046094	1/2

Vztah mezi pojmy magnetický moment a magnetizace viz magnetizace.