Světelné hodiny

Světelné hodiny jsou jednoduchým způsobem, jak ukázat základní rys speciální teorie relativity. Hodiny fungují tak, že odrazí záblesk světla od vzdáleného zrcadla a pomocí jeho návratu spustí další záblesk světla, přičemž se mezitím počítá, kolik záblesků po cestě proběhlo. Je snadné ukázat, že lidé na Zemi sledující kosmickou loď letící nad hlavou s takovými hodinami by viděli, že tikají relativně pomalu. Tento efekt se nazývá dilatacečasu.

Než se začneme zabývat světelnými hodinami, uvažujme o jiném druhu relativity. Představte si, že někdo dribluje s basketbalovým míčem v nákladovém prostoru velkého dopravního letadla. Basketbalista se pohybuje stejným směrem jako tryskové letadlo. Ostatní lidé v letadle vidí, jak se při jednom driblování pohybuje o metr nebo dva. Mezi prvním a druhým odrazem míče uplyne přibližně jedna sekunda. Ale když došlo k prvnímu odrazu, byl basketbalový míč nad Gibraltarem, a když došlo k druhému odrazu, byl basketbalový míč nad vodou blíže Španělsku. Basketbalový míč se tedy vůči Zemi posunul o 280 metrů.

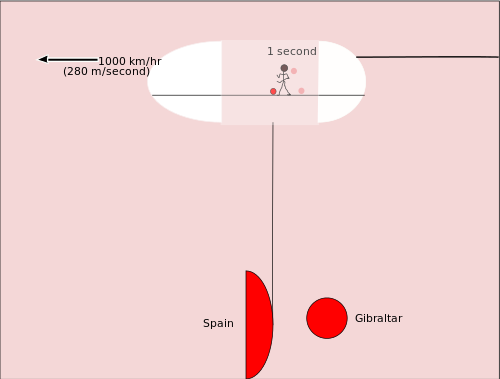
Nyní se zamyslete nad poněkud podobnou otázkou relativního pohybu. Tentokrát se budeme zabývat tím, co vidí lidé, kteří se dívají na hvězdy ze severního pólu, když nad nimi prolétá velmi rychlá kosmická loď. Pomocí algebry a Pythagorovy věty můžeme spočítat, o kolik se zpomalí čas kosmické lodi. Jediné, co ještě potřebujeme, je rovnice, která spojuje vzdálenost, d, rychlost neboli rychlost letu, r, a čas, t. Rovnice zní:

d = rt

Rychlost světla je konstantní, takže tuto hodnotu použijeme na dva problémy. Rychlost světla budeme nazývat c, protože toto písmeno vědci obvykle používají pro její pojmenování.

Hodiny se vyrobí tak, že se na spodní část dlouhé tyče umístí světelný výstup, na vrchol tyče se umístí zrcadlo a na spodní část tyče se umístí elektronický detektor světla. Hodiny se spustí krátkým sepnutím spínače, který vyšle jeden záblesk světla ze spodní části sloupu na vrchol sloupu, kde se odrazí zpět na spodní část sloupu. Když detektor světla ve spodní části sloupu uvidí světelný záblesk, provede dvě věci. Přičte jedničku k počítadlu, které je k němu připojeno, a vystřelí další světelný záblesk nahoru k zrcadlu. Jakmile se toto bliknutí světla vrátí zpět k dolní části, změní se počet na dva a spustí se další bliknutí světla. Protože se světlo šíří velmi rychle (300 000 km/s), za každou sekundu měřenou běžnými hodinami "tiknou" světelné hodiny velmi mnohokrát.

Pro snazší počítání řekneme, že tyč je dlouhá půl kilometru. Pokud tedy stojíme u světelných hodin, které jsou postaveny vedle velkého dalekohledu na severním pólu, uvidíme, že světlo urazí jeden kilometr za každé "tiknutí" světelných hodin. Protože uražená vzdálenost d se rovná rychlosti vynásobené časem a příslušná rychlost je c, máme rovnici:

d = ct

a tuto rovnici můžeme vyřešit pro t, abychom zjistili, jak dlouho v sekundách trvá každé "tiknutí".

1 km = 300 000 km/sekundu * t sekund

t sekund = 1 km/300 000 (km/sekundu) = 1/300 000 sekund = 0,00000333...3 sekund

Jinými slovy, každé "tiknutí" světelných hodin bude trvat 0,00000333...3 sekundy.

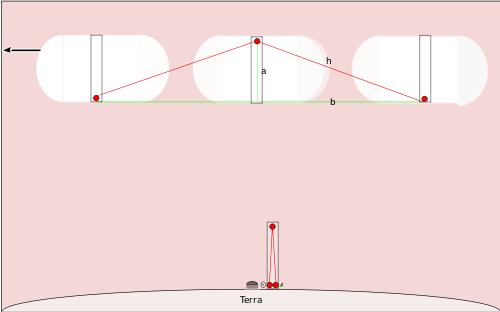
Kdyby vesmírná loď letěla po přímce nad severním pólem velkou částí rychlosti světla a měla podobné hodiny, lidé sledující její průlet by viděli, že zrcadlo na vrcholu pólu se posunulo přímo nad vyzařující světlo, takže světlo by se pohybovalo po přímce označené h v diagramu a pak by se po druhé hypotenuse vrátilo zpět dolů k základně pólu - ta by se mezitím posunula o určitou vzdálenost, protože vesmírná loď se pohybuje tak rychle. Můžeme si spočítat, kolik času by podle lidí na Zemi trvalo jedno tiknutí. Víme, že pól kosmické lodi má délku a, protože se jedná o stejný druh hodin, jaké používají lidé na severním pólu. Chceme zjistit t' , dobu, za kterou na kosmické lodi proběhne jedno tiknutí hodin.

Víme, že kosmická loď urazí 1/2 r t', když světelný záblesk směřuje nahoru k zrcadlu, a další 1/2 r t', když světelný záblesk směřuje dolů k základně sloupu. Tento výpočet nám tedy dává délku přímky b v grafu. Známe a, takže můžeme vypočítat h pomocí Pythagorovy věty:

h = √(a2 + (rt' /2)²)

Celková vzdálenost, kterou světlo urazí, je tedy 2 h neboli d = 2 √(a2 + (rt' /2)²).

Víme také, že rychlost světla c je konstantní. Ať ji měří kdokoli, ukazuje se, že je to stejná rychlost. Tuto skutečnost tedy můžeme využít k jinému způsobu výpočtu, jak dlouho trvá záblesku světla, než se dostane ze základny na vrchol tyče a zpět:

t' = d/c

Jinými slovy, d = c t' .

Můžeme tedy napsat

c t' = 2 √(a2 + (rt' /2)²)

nebo

1/2 c t' = √(a2 + (rt' /2)²)

K vyřešení výše uvedené rovnice budeme potřebovat:

1. Čtverec na obou stranách
2. Obě strany vydělte t' ²
3. Obě strany vynásobte 4
4. Obě strany vydělte číslem c2
5. Zjednodušte c2 / c2
6. Odečtěte r2/c2 od obou stran
7. Vezměte druhou odmocninu z obou stran
8. Obě strany vynásobte t'
9. Obě strany vydělte √(1-r2/c2)

Řešením výše uvedené rovnice zjistíme, že:

t' = 2a/(c√(1-r2/c2)

Čas mezi tiky hodin na severním pólu je 2a/c, takže můžeme napsat:

t' = t/√(1-r2/c2)

Jestliže t = 1 sekunda, pak pokud se kosmická loď pohybuje poloviční rychlostí světla, t' = 1,1547 s.

Experimentujte s různými rychlostmi jízdy na adrese: http://www.1728.org/reltivty.htm.

Otázky a odpovědi

Otázka: Co jsou to světelné hodiny?

Otázka: Co je to dilatace času?

Otázka: Jak můžeme vypočítat, o kolik se čas na kosmické lodi zpomalí?

Otázka: Jak fungují světelné hodiny?

Otázka: Jakou rovnici potřebujeme pro tento výpočet?

Otázka: Jak souvisí Pythagorova věta s tímto výpočtem?

Hledání podle dopisu