Keplerovy zákony
Keplerovy zákony pohybu planet jsou tři zákony, které popisují pohyb planet kolem Slunce:
- Planety se pohybují kolem Slunce po eliptických drahách. Slunce se nachází v jednom ze dvou ohnisek dráhy.
- Úsečka spojující planetu a Slunce vymetá ve stejných časových intervalech stejné plochy.
- Čtverec oběžné doby planety je úměrný krychli poloosy její dráhy.
Tyto zákony objevil Johannes Kepler v letech 1609 až 1619.
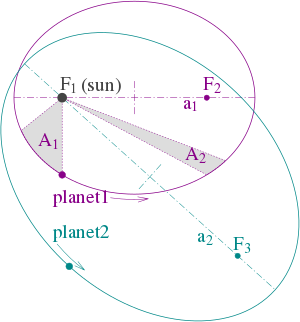
Obrázek 1: Znázornění tří Keplerových zákonů na dvou planetárních drahách. (1) Oběžné dráhy jsou elipsy s ohnisky ƒ1 a ƒ2 pro první planetu a ƒ1 a ƒ3 pro druhou planetu. Slunce je umístěno v ohnisku ƒ1 . (2) Dva zastíněné sektory A1 a A2 mají stejný povrch a čas, za který planeta 1 pokryje segment A1 , je roven času, za který pokryje segment A2 . (3) Celkové doby oběhu planety 1 a planety 2 mají poměr a13/2 : a23/2 .
Srovnání s Koperníkem
Keplerovy zákony vylepšují Koperníkův model. Pokud se excentricity planetárních drah považují za nulové, pak Kepler v podstatě souhlasí s Koperníkem:
- Oběžná dráha planety je kružnice
- Slunce ve středu dráhy
- Rychlost planety na oběžné dráze je konstantní.
Excentricity oběžných drah planet známých Koperníkovi a Keplerovi jsou malé, takže výše uvedená pravidla poskytují dobré aproximace pohybu planet; Keplerovy zákony však odpovídají pozorováním lépe než Koperníkovy.
Keplerovy opravy nejsou vůbec zřejmé:
- Oběžná dráha planety není kružnice, ale elipsa.
- Slunce není ve středu, ale v ohnisku eliptické dráhy.
- Lineární ani úhlová rychlost planety na oběžné dráze není konstantní, ale plošná rychlost je konstantní.
Excentricita oběžné dráhy Země způsobuje, že doba od březnové rovnodennosti do zářijové rovnodennosti, přibližně 186 dní, je nerovná době od zářijové rovnodennosti do březnové rovnodennosti, přibližně 179 dní. Průměr by rozdělil dráhu na stejné části, ale rovina procházející Sluncem rovnoběžně se zemským rovníkem rozděluje dráhu na dvě části s plochami v poměru 186 ku 179, takže excentricita dráhy Země je přibližně stejná jako excentricita Slunce.
ε ≈ π 4 186 - 179 186 + 179 ≈ 0,015 , {\displaystyle \varepsilon \aprox {\frac {\pi }{4}}{\frac {186-179}{186+179}}\aprox 0,015,}
která se blíží správné hodnotě (0,016710219) (viz dráha Země). Výpočet je správný, pokud perihelium, tedy datum, kdy je Země nejblíže Slunci, připadá na slunovrat. Současné perihelium, které je blízko 4. ledna, je poměrně blízko slunovratu 21. prosince.
Vyhledávání
