Paralelní postulát
V geometrii je paralelní postulát jedním z axiomů euklidovské geometrie. Někdy se mu také říká pátý Euklidův postulát, protože je pátým postulátem v Euklidových Elementech.
Postulát říká, že:
Pokud úsečku protnete dvěma přímkami a oba vnitřní úhly, které tyto přímky svírají, jsou menší než 180°, pak se obě přímky nakonec setkají, pokud je dostatečně prodloužíte.
Obor geometrie, který se řídí všemi Euklidovými axiomy, se nazývá euklidovská geometrie. Geometrie, která se neřídí všemi Euklidovými axiomy, se nazývá neeuklidovská geometrie.
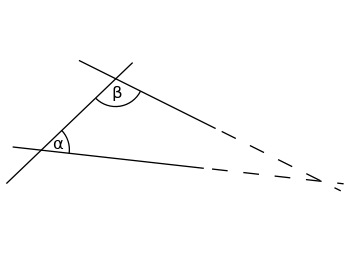
Je-li součet vnitřních úhlů α (alfa) a β (beta) menší než 180°, obě přímky se někde protnou, pokud jsou obě prodlouženy do nekonečna.
Historie
Někteří matematici se domnívali, že Euklidův pátý postulát je mnohem delší a složitější než ostatní čtyři postuláty. Mnozí z nich se domnívali, že jej lze dokázat z ostatních jednodušších axiomů. Někteří matematici prohlásili, že tento postulát dokázali z jednodušších postulátů, ale ukázalo se, že se všichni mýlili.
Playfairův axiom
Další novější věta známá jako Playfairův axiom je podobná Euklidovu pátému postulátu. Říká, že:
Je dána přímka a bod, který na této přímce neleží, a tímto bodem lze nakreslit pouze jednu přímku, která se nepotká s druhou přímkou.
Ve skutečnosti matematici zjistili, že tento axiom je nejen podobný Euklidovu pátému postulátu, ale má úplně stejné důsledky. Z matematického hlediska se obě věty nazývají "ekvivalentní" věty. Dnes je Playfairův axiom matematiky používán častěji než původní Euklidův paralelní postulát.
Neeuklidovská geometrie
Nakonec se někteří matematici pokusili vytvořit nové geometrie bez použití axiomu. Jeden z druhů neeuklidovské geometrie se nazývá eliptická geometrie. V eliptické geometrii je paralelní postulát nahrazen axiomem, který říká, že:
Pokud je dána přímka a bod, který na ní neleží, nelze tímto bodem nakreslit přímku, která by nakonec neprotínala druhou přímku.
Matematici zjistili, že když nahradili Euklidův pátý postulát tímto axiomem, byli stále schopni dokázat mnoho dalších Euklidových tvrzení. Jedním ze způsobů, jak si představit eliptickou geometrii, je představit si povrch zeměkoule. Na glóbu se zdá, že přímky zeměpisné délky jsou na rovníku rovnoběžné, ale všechny se setkávají na pólech. Koncem 19. století se ukázalo, že eliptická geometrie je konzistentní. Tím se prokázalo, že Euklidův pátý postulát není nezávislý na ostatních postulátech. Poté se matematici většinou přestali snažit dokázat pátý postulát z ostatních čtyř postulátů. Místo toho mnozí matematici začali studovat jiné geometrie, které se Euklidovým pátým postulátem neřídí.
Další axiom, kterým matematici někdy nahrazují Euklidův pátý axiom, říká, že:
Pokud je dána přímka a bod, který na ní neleží, můžete tímto bodem nakreslit alespoň dvě přímky, které nakonec neprotnou druhou přímku.
Tomu se říká hyperbolická geometrie.
Jiná geometrie pouze odstraňuje Euklidův pátý postulát a ničím ho nenahrazuje. Tato geometrie se nazývá neutrální geometrie nebo absolutní geometrie.
Vyhledávání