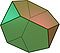
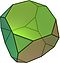
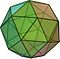
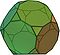
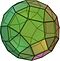
Archimédovské těleso
Archimédovo těleso je v geometrii konvexní útvar složený z mnohoúhelníků. Je to mnohostěn s následujícími vlastnostmi:
- Každá strana je tvořena pravidelným mnohoúhelníkem
- Všechny rohy tvaru vypadají stejně.
- Tento tvar není ani platónské těleso, ani hranol, ani antihranol.
Podle toho, jak se počítají, je takových tvarů třináct nebo patnáct. Ze dvou z těchto útvarů existují dvě verze, které se nedají shodovat pomocí otáčení. Archimédova tělesa jsou pojmenována po starořeckém matematikovi Archimédovi, který je objevil pravděpodobně ve 3. století př. n. l.. Archimédovy spisy se ztratily, ale ve 4. století je shrnul Pappus z Alexandrie. V období renesance umělci a matematici oceňovali čisté formy a všechny tyto formy znovu objevili. Johannes Kepler toto hledání pravděpodobně dokončil kolem roku 1620.
Ke konstrukci archimédovského tělesa je třeba alespoň dvou různých mnohoúhelníků.
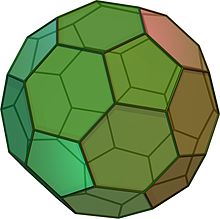
Zkrácený ikosaedr vypadá jako fotbalový míč. Skládá se z 12 rovnostranných pětiúhelníků a 20 pravidelných šestiúhelníků. Má 60 vrcholů a 90 hran. Je to archimédovské těleso
Vlastnosti
- Archimédova tělesa jsou tvořena pravidelnými mnohoúhelníky, proto mají všechny hrany stejnou délku.
- Všechna archimédovská tělesa lze vytvořit z platónských těles "seříznutím hran" platónského tělesa.
- Typ mnohoúhelníků, které se setkávají v rohu ("vrcholu"), charakterizuje archimédovská i platónská tělesa.
Vztah k platónským tělesům
Platónská tělesa lze přeměnit na archimédovská tělesa podle řady pravidel pro jejich konstrukci.
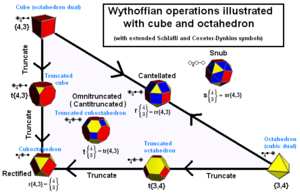
Archimédova tělesa lze konstruovat jako pozice generátoru v kaleidoskopu.
Seznam Archimédových těles
Následuje seznam všech Archimédových těles.
| Obrázek | Název | Tváře | Typ | Hrany | Vrcholy |
|
| Zkrácený čtyřstěn | 8 | 4 trojúhelníky 4 šestiúhelníky | 18 | 12 |
|
| 14 | 8 trojúhelníků 6 čtverců | 24 | 12 | |
|
| Zkrácená krychle | 14 | 8 trojúhelníků 6 osmiúhelníků | 36 | 24 |
|
| Zkrácený osmistěn | 14 | 6 čtverců 8 šestiúhelníků | 36 | 24 |
|
| Rhombicuboctahedron | 26 | 8 trojúhelníků 18 čtverců | 48 | 24 |
|
| Zkrácený kuboktaedr | 26 | 12 čtverců 8 šestiúhelníků 6 osmiúhelníků | 72 | 48 |
|
| Kostka Snub (2 zrcadlové verze) | 38 | 32 trojúhelníků 6 čtverců | 60 | 24 |
|
| Ikosidodekaedr | 32 | 20 trojúhelníků 12 pětiúhelníků | 60 | 30 |
|
| Zkrácený dvanáctistěn | 32 | 20 trojúhelníků 12 dekagonů | 90 | 60 |
|
| Zkrácený ikosaedr | 32 | 12 pětiúhelníků 20 šestiúhelníků | 90 | 60 |
|
| Rhombicosidodecahedron | 62 | 20 trojúhelníků30 čtverců12 | 120 | 60 |
|
| Zkrácený ikosidodekaedr | 62 | 30 čtverců 20 šestiúhelníků 12 dekagonů | 180 | 120 |
|
| Snub dodekaedr (2 zrcadlové verze) | 92 | 80 trojúhelníků 12 pětiúhelníků | 150 | 60 |
Otázky a odpovědi
Otázka: Co je to archimédovské těleso?
Odpověď: Archimédovo těleso je konvexní útvar složený z mnohoúhelníků, který má ty vlastnosti, že každá jeho stěna je pravidelný mnohoúhelník, všechny rohy vypadají stejně a není to platónské těleso, hranol ani antihranol.
Otázka: Kolik je archimédovských těles?
Odpověď: Podle toho, jak je počítáme, existuje buď třináct, nebo patnáct archimédovských těles.
Otázka: Kdo objevil Archimédova tělesa?
Odpověď: Archimédova tělesa jsou pojmenována po starořeckém matematikovi Archimédovi, který je objevil pravděpodobně ve 3. století př. n. l..
Otázka: Co udělal Pappus Alexandrijský s Archimédovými spisy?
Odpověď: Pappus Alexandrijský shrnul Archimédovy spisy o Archimédových tělesech ve 4. století.
Otázka: Proč umělci a matematici znovu objevili Archimédova tělesa v období renesance?
Odpověď: V renesanci si umělci a matematici cenili čistých forem a Archimédova tělesa byla považována za čisté formy.
Otázka: Kdy Johannes Kepler dokončil hledání všech archimédovských těles?
Odpověď: Johannes Kepler pravděpodobně dokončil hledání všech Archimédových těles kolem roku 1620.
Otázka: Co je potřeba k sestrojení Archimédova tělesa?
Odpověď: Sestrojení Archimédova tělesa vyžaduje alespoň dva různé mnohoúhelníky.
Vyhledávání