Eulerův vzorec
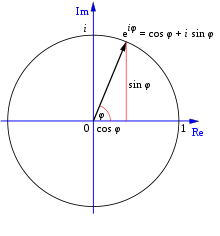
Eulerův vzorec, který se někdy nazývá Eulerův vztah, je rovnice v analýze. Vytváří vztah mezi trigonometrickými funkcemi a exponenciálními funkcemi komplexních čísel. Je pojmenována po Leonhardu Eulerovi, který ji publikoval v roce 1748. Když ji Euler publikoval, uvedl, že úhel musí být reálné číslo. Později se ukázalo, že vzorec funguje i v případě, že úhel není reálné číslo, ale komplexní.
Otázky a odpovědi
Otázka: Co je to Eulerův vzorec?
Odpověď: Eulerův vzorec je rovnice zahrnující komplexní čísla a trigonometrické funkce, která vztahuje exponenciální funkce komplexních čísel k trigonometrickým funkcím.
Otázka: Kdo publikoval Eulerův vzorec?
Odpověď: Leonhard Euler publikoval Eulerův vzorec v roce 1748.
Otázka: Funguje vzorec, když úhel není reálné číslo?
Odpověď: Ano, ukázalo se, že vzorec funguje i v případě, že úhel je komplexní číslo.
Otázka: Co se stane, když je úhel pí?
Odpověď: Když je úhel pí, Eulerův vzorec se změní na e^iנ = -1.
Otázka: Co se stane, když je úhel 2pi?
Odpověď: Když je úhel 2pi, Eulerův vzorec je e^i2נ = 1.
Otázka: Co v této rovnici představuje písmeno "e"?
Odpověď: V této rovnici představuje "e" Eulerovo číslo.
Otázka: Co v této rovnici představuje "i"?
O: V této rovnici představuje "i" imaginární jednotku.
Vyhledávání