Konjugované proměnné
Konjugované proměnné jsou speciální dvojice proměnných (např. x, y, z), které při určité matematické operaci nedávají stejný výsledek. To znamená, že x*y se nerovná y*x. Písmeno * zde neznamená násobení. Může znamenat sčítání, odčítání, dělení nebo jakoukoli operaci, která má v tomto případě smysl.
Fyzik Werner Heisenberg a jeho spolupracovníci použili rovnice studované v klasické fyzice k popisu a předpovědi událostí z kvantové fyziky. Zjistil, že hybnost (hmotnost krát rychlost, reprezentovaná P) a poloha (reprezentovaná Q) jsou konjugované veličiny. To znamená, že P*Q se v kvantové fyzice nerovná Q*P.
Zde jsou dvě speciální rovnice pro výpočet energie elektronu (malé zelené věci) v atomu vodíku.
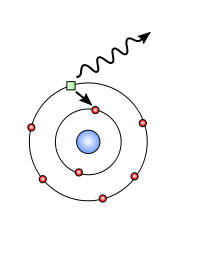
První rovnici lze použít ke zjištění součinu hybnosti a polohy:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{}\,p(n,n-a)q(n-a,n-b)}
Druhou rovnici lze použít k výpočtu součinu polohy a hybnosti:
Z ( n , n - b ) = ∑ a q ( n , n - a ) p ( n - a , n - b ) {\displaystyle Z(n,n-b)=\sum _{a}^{}\,q(n,n-a)p(n-a,n-b)}
O něco později jiný fyzik, Max Born, zjistil, že protože P*Q se nerovná Q*P, výsledek Q*P minus P*Q není nulový. ("Mínus" není stejné mínus jako "3 - 2". Je to jiná věc se stejným názvem).
Born zjistil, že:
Q ∗ P - P ∗ Q = i h 2 π {\displaystyle {Q*P-P*Q={\frac {ih}{2\pi }}}}
[Symbol Q je matice pro polohu, P je matice pro hybnost, i je komplexní číslo a h je Planckova konstanta, číslo, které se často objevuje v kvantové mechanice.]
Konjugované proměnné se používají v celé fyzice, chemii a mnoha dalších vědních oborech.
Některá související témata
Otázky a odpovědi
Otázka: Co jsou konjugované proměnné?
Odpověď: Konjugované proměnné jsou speciální dvojice proměnných (např. x, y, z), které nedávají stejný výsledek, když s nimi provedete určitou matematickou operaci. To znamená, že x*y se nerovná y*x.
Otázka: Kdo objevil konjugované proměnné?
Odpověď: Fyzik Werner Heisenberg a jeho spolupracovníci použili rovnice studované v klasické fyzice k popisu a předpovědi událostí z kvantové fyziky. Objevil, že hybnost (hmotnost krát rychlost, reprezentovaná P) a poloha (reprezentovaná Q) jsou konjugované veličiny.
Otázka: Jakou rovnici lze použít k výpočtu součinu hybnosti a polohy?
Odpověď: K určení součinu hybnosti a polohy lze použít první rovnici: Y(n,n-b)=∑a p(n,n-a)q(n-a,n-b).
Otázka: Jakou rovnici lze použít k výpočtu součinu polohy a hybnosti?
Odpověď: K výpočtu součinu polohy a hybnosti lze použít druhou rovnici: Z(n,n-b)=∑a q(n,n-a)p(n-a, n-b).
Otázka: Co objevil Max Born o konjugovaných proměnných?
Odpověď: Max Born zjistil, že protože P*Q se nerovná Q*P, výsledek Q*P minus P*Q není nulový. Také zjistil, že Q-P - P-Q = ih/2π.
Otázka: Jak se Planckova konstanta projevuje v kvantové mechanice?
Odpověď: Planckova konstanta se v kvantové mechanice objevuje často, protože se objevuje v rovnici Maxe Borna pro výpočet součinů konjugovaných proměnných; konkrétně jako h/2π na jedné straně znaménka rovnosti.
Otázka: V jakých oblastech se konjugované proměnné používají?
Odpověď: Konjugované proměnné mají uplatnění v celé fyzice, chemii a dalších oblastech vědy.
Vyhledávání


