Minkowského prostoročas
Minkowského prostoročas je ve speciální teorii relativity čtyřrozměrný mnohostěn, který vytvořil Hermann Minkowski. Má čtyři rozměry: tři rozměry prostoru (x, y, z) a jeden rozměr času. Minkowského prostoročas má metrickou signaturu (-+++) a popisuje plochý povrch, pokud není přítomna žádná hmota. V tomto článku je zvykem nazývat Minkowského prostoročas jednoduše prostoročas.
Minkowského prostoročas však platí pouze ve speciální teorii relativity. Obecná relativita používá pojem zakřiveného prostoročasu k popisu účinků gravitace a zrychleného pohybu.
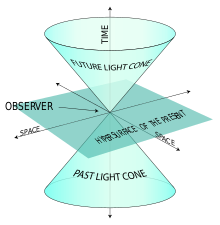
Příklad světelného kužele.
Definice
Matematické
Časoprostor si lze představit jako čtyřrozměrný souřadnicový systém, jehož osy jsou dány vztahem
( c t , x , y , z ) {\displaystyle (ct,x,y,z)}
Lze je také označit
( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})}
Kde x 1 {\displaystyle x_{1}}

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}}
Z toho vyplývá, že prostoročas má metrický tenzor daný vztahem
g u v = [ - 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\0&1&0&0\0&0&0&1&0\0&0&0&0&1\end{bmatrix}}}
Jak již bylo řečeno, časoprostor je všude plochý; do jisté míry si jej lze představit jako rovinu.
Jednoduché
Časoprostor si lze představit jako "arénu", v níž se odehrávají všechny události ve vesmíru. Vše, co potřebujeme k určení bodu v časoprostoru, je určitý čas a typická prostorová orientace. Představit si čtyři rozměry je obtížné (prakticky nemožné), ale určitou analogii lze vytvořit pomocí níže uvedené metody.
Časoprostorové diagramy
Hermann Minkowski zavedl určitou metodu pro grafické znázornění souřadnicových systémů v Minkowského prostoročase. Jak je vidět vpravo, různé souřadnicové systémy se neshodnou na prostorové orientaci a/nebo poloze objektu v čase. Jak je vidět z grafu, existuje pouze jedna prostorová osa (osa x) a jedna časová osa (osa ct). V případě potřeby lze zavést další prostorovou dimenzi (osa y); bohužel to je limitní počet dimenzí: grafické znázornění ve čtyřech dimenzích je nemožné. Pravidlo pro vykreslování grafů v Minkowského prostoročase je následující:
1) Úhel mezi osou x a osou x'je dán vztahem t a n ( α ) = v c {\displaystyle tan(\alfa )={\frac {v}{c}}}
2) Rychlost světla v časoprostoru svírá s oběma osami vždy úhel 45 stupňů.
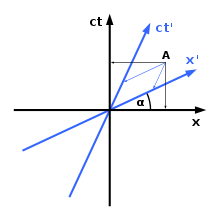
V teorii relativity oba pozorovatelé přiřazují událost v bodě A různým časům.
Časoprostor v obecné relativitě
V obecné teorii relativity použil Einstein rovnici.
R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}}
Umožnit skutečné zakřivení časoprostoru; výsledné účinky jsou účinky gravitace.
Související stránky
- Časoprostor
- Speciální teorie relativity
- Obecná relativita
| Kontrola úřadu |
|
Otázky a odpovědi
Otázka: Co je to Minkowského prostoročas?
Odpověď: Minkowského prostoročas je čtyřrozměrný mnohostěn vytvořený Hermannem Minkowským. Má tři rozměry prostoru (x, y, z) a jeden rozměr času.
Otázka: Jaká je metrická signatura Minkowského prostoročasu?
Odpověď: Metrická signatura Minkowského prostoročasu je (-+++).
Otázka: Jak Minkowského prostoročas popisuje plochý povrch?
Odpověď: Pokud není přítomna žádná hmota, popisuje Minkowského prostoročas plochý povrch.
Otázka: Platí Minkowského prostoročas pro obecnou teorii relativity?
Odpověď: Ne, Minkowského prostoročas platí pouze ve speciální teorii relativity. Obecná relativita používá pojem zakřiveného prostoročasu k popisu účinků gravitace a zrychleného pohybu.
Otázka: Kolik rozměrů má Minkowsiho prostoročas?
Odpověď: Minkowsiho prostoročas má čtyři rozměry - tři rozměry prostoru (x, y, z) a jeden rozměr času.
Otázka: Kdo vytvořil koncept Minkowsiho prostoročasu?
Odpověď: Hermann Minkowksi vytvořil koncept MInkowského prostoročasu.
Vyhledávání




