Lineární regrese
Lineární regrese je způsob, jak vysvětlit vztah mezi závislou proměnnou a jednou nebo více vysvětlujícími proměnnými pomocí přímky. Jedná se o zvláštní případ regresní analýzy.
Lineární regrese byla prvním typem regresní analýzy, který byl důsledně studován. Je to proto, že modely, které jsou lineárně závislé na svých neznámých parametrech, se snáze přizpůsobují než modely, které jsou se svými parametry spojeny nelineárně. Navíc se snáze určují statistické vlastnosti výsledných odhadů.
Lineární regrese má mnoho praktických využití. Většina aplikací spadá do jedné ze dvou následujících kategorií:
- Lineární regresi lze použít k přiřazení predikčního modelu k souboru pozorovaných hodnot (dat). To je užitečné, pokud je cílem předpověď, prognóza nebo redukce. Pokud je po vytvoření takového modelu následně zadána další hodnota X bez doprovodné hodnoty y, lze fitovaný model použít k předpovědi hodnoty y.
- Vzhledem k proměnné y a řadě proměnných X1, ..., Xp, které mohou souviset s y, lze lineární regresní analýzu použít ke kvantifikaci síly vztahu mezi y a Xj, k posouzení, které Xj nemají vůbec žádný vztah k y, a k určení, které podmnožiny Xj obsahují nadbytečné informace o y.
Lineární regresní modely se snaží, aby vertikální vzdálenost mezi přímkou a datovými body (např. reziduálními hodnotami) byla co nejmenší. Tomu se říká "přizpůsobení přímky datům". Lineární regresní modely se často snaží minimalizovat součet čtverců reziduí (nejmenší čtverce), ale existují i jiné způsoby přizpůsobení. Patří mezi ně minimalizace "neshodnosti" v nějaké jiné normě (jako u regrese nejmenších absolutních odchylek) nebo minimalizace penalizované verze ztrátové funkce nejmenších čtverců jako u hřebenové regrese. Přístup nejmenších čtverců lze použít i k fitování modelů, které nejsou lineární. Jak bylo nastíněno výše, pojmy "nejmenší čtverce" a "lineární model" spolu úzce souvisejí, ale nejsou to synonyma.
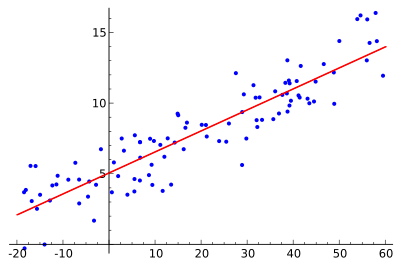
Cílem je najít červenou křivku, modré body jsou skutečné vzorky. U lineární regrese lze všechny body spojit jedinou přímkou. Tento příklad používá jednoduchou lineární regresi, kde se minimalizuje čtverec vzdálenosti mezi červenou přímkou a každým bodem vzorku.
Použití
Ekonomika
Lineární regrese je hlavním analytickým nástrojem v ekonomii. Používá se například k odhadu výdajů na spotřebu, výdajů na fixní investice, investic do zásob, nákupů vývozů dané země, výdajů na dovozy, poptávky po likvidních aktivech, poptávky po práci a nabídky práce.
Otázky a odpovědi
Otázka: Co je to lineární regrese?
Odpověď: Lineární regrese je způsob, jak pomocí matematiky sledovat, jak se něco mění, když se mění jiné věci. Používá závislou proměnnou a jednu nebo více vysvětlujících proměnných k vytvoření přímky, známé jako "regresní přímka".
Otázka: Jaké jsou výhody lineární regrese?
Odpověď: Modely, které jsou lineárně závislé na svých neznámých parametrech, se snáze přizpůsobují než modely, které jsou se svými parametry spojeny nelineárně. Kromě toho se snáze určují statistické vlastnosti výsledných odhadů.
Otázka: Jaké je praktické využití lineární regrese?
Odpověď: Lineární regresi lze použít k přiřazení predikčního modelu k pozorovaným hodnotám (datům) za účelem předpovědí, prognóz nebo redukcí. Lze ji také použít ke kvantifikaci síly vztahů mezi proměnnými a k identifikaci podmnožin dat, které obsahují nadbytečné informace o jiné proměnné.
Otázka: Jak se lineární regresní modely snaží minimalizovat chyby?
Odpověď: Lineární regresní modely se snaží, aby vertikální vzdálenost mezi přímkou a datovými body (rezidua) byla co nejmenší. Toho se dosahuje minimalizací buď součtu čtverců reziduí (nejmenší čtverce), nedostatku shody v nějaké jiné normě (nejmenší absolutní odchylky), nebo minimalizací penalizované verze ztrátové funkce nejmenších čtverců (hřebenová regrese).
Otázka: Je možné, aby modely lineární regrese nebyly založeny na metodě nejmenších čtverců?
Odpověď: Ano, je možné, aby lineární regresní modely nebyly založeny na metodě nejmenších čtverců, ale místo toho používaly metody, jako je minimalizace neshodnosti v nějaké jiné normě (nejmenší absolutní odchylky) nebo minimalizace penalizované verze ztrátové funkce nejmenších čtverců (hřebenová regrese).
Otázka: Jsou "lineární model" a "nejmenší čtverce" synonyma?
Odpověď: Ne, nejsou to synonyma. Ačkoli spolu úzce souvisejí, "lineární model" se týká konkrétně použití přímky, zatímco "nejmenší čtverce" se týkají konkrétně snahy minimalizovat chyby tím, že se zajistí minimální vertikální vzdálenost mezi přímkou a datovými body.
Vyhledávání