Heavisideova funkce
Heavisideova funkce H je nespojitá funkce, jejíž hodnota je nula pro záporný vstup a jedna pro kladný vstup.
Funkce se v matematice teorie řízení používá k vyjádření signálu, který se zapne v určitém čase a zůstane zapnutý po neomezenou dobu. Byla pojmenována po Angličanovi Oliveru Heavisidovi.
Heavisideova funkce je integrál Diracovy delta funkce: H′ = δ. Někdy se zapisuje jako
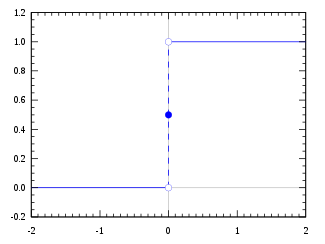
Heavisideova kroková funkce s použitím konvence polovičního maxima
Diskrétní forma
Můžeme také definovat alternativní tvar Heavisidovy krokové funkce jako funkci diskrétní proměnné n:
H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}
kde n je celé číslo.
Nebo
H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)}
Jednotkový impuls v diskrétním čase je první rozdíl kroku v diskrétním čase.
δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1]. }
Tato funkce je kumulativním součtem Kroneckerovy delty:
H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}
kde
δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0}\,}
je diskrétní jednotková impulsní funkce.
Zastoupení
Často je užitečná integrální reprezentace Heavisidovy krokové funkce:
H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e i x τ d τ . {\displaystyle H(x)=\lim _{\epsilon \to 0^{+}}-{1 \nad 2\pi \mathrm {i}. }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau . } 
H(0)
Hodnotu funkce v bodě 0 lze definovat jako H(0) = 0, H(0) = ½ nebo H(0) = 1.
H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} 
Související stránky
- Laplaceova transformace
Otázky a odpovědi
Otázka: Co je to Heavisideova funkce?
Odpověď: Heavisideova funkce je nespojitá funkce, jejíž hodnota je nula pro záporný vstup a jedna pro kladný vstup.
Otázka: Proč se Heavisidova funkce používá v teorii řízení?
Odpověď: Heavisidova funkce se v teorii řízení používá k vyjádření signálu, který se zapne v určitém čase a zůstane zapnutý po neomezenou dobu.
Otázka: Po kom byla Heavisidova funkce pojmenována?
Odpověď: Heavisidova funkce byla pojmenována po Angličanovi Oliveru Heavisidovi.
Otázka: Jaký je vztah mezi Heavisidovou funkcí a Diracovou funkcí delta?
Odpověď: Heavisidova funkce je integrál Diracovy funkce delta: H′(x)= δ(x).
Otázka: Jaký je výstup Heavisideovy funkce pro kladné vstupy?
Odpověď: Heavisideova funkce je pro kladné vstupy jedničkou.
Otázka: Jaký je výstup Heavisidovy funkce pro záporné vstupy?
Odpověď: Heavisideova funkce je pro záporné vstupy nulová.
Otázka: Jaký typ funkce je Heavisideova funkce?
Odpověď: Heavisideova funkce je nespojitá funkce.
Vyhledávání
![{\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}](https://www.alegsaonline.com/image/efb65c686bdec46712eae1997c363f7ef8709b79.svg)

![{\displaystyle \delta \left[n\right]=H[n]-H[n-1].}](https://www.alegsaonline.com/image/e6c417f161a7987a4db18818743eeb23494b0feb.svg)
![{\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}](https://www.alegsaonline.com/image/5db28db3163e2940aaf93d0fc180edb19d865d32.svg)
![{\displaystyle \delta [k]=\delta _{k,0}\,}](https://www.alegsaonline.com/image/97a99ab7d257c74f38fbb2d42c8e42e1cb16d0e9.svg)