Bernoulliho–Navierova hypotéza

Eulerova-Bernoulliho teorie nosníků (známá také jako inženýrská teorie nosníků nebo klasická teorie nosníků) je jednoduchá metoda výpočtu ohybu nosníků při zatížení. Platí pro malé průhyby (o kolik se něco posune) nosníku bez uvažování účinků smykových deformací. Proto ji lze považovat za zvláštní případ Timošenkovy teorie nosníků. Poprvé byla zavedena kolem roku 1750. Popularitu si získala během vývoje Eiffelovy věže a ruského kola na konci 19. století. Poté se používala v mnoha technických oborech včetně strojírenství a stavebnictví. Přestože byly vyvinuty další pokročilé metody, Eulerova-Bernoulliho teorie nosníků je pro svou jednoduchost stále hojně využívána.

Vibrující skleněný nosník znázorňující ohyb nosníků, který lze odhadnout pomocí Eulerovy-Bernoulliho teorie nosníků.

Historie

Jako první tuto teorii sestavili v roce 1750 Leonhard Euler a Daniel Bernoulli. V té době se na vědu a techniku pohlíželo jinak než dnes. Matematickým teoriím, jako byla Eulerova-Bernoulliho teorie paprsků, se pro praktické inženýrské využití nedůvěřovalo. Mosty a budovy se navrhovaly stejnými metodami až do konce 19. století. Tehdy Eiffelova věž a ruské kolo ukázaly platnost teorie ve větším měřítku.

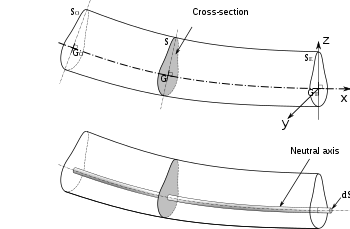
Kresba příčného řezu ohýbaného nosníku se znázorněním neutrální osy

Statická rovnice nosníku

Eulerova-Bernoulliho rovnice popisuje vztah mezi průhybem nosníku a působícím zatížením, jak je uvedeno níže:

d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}\right)=q\,} ${\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,$

Kde w ( x ) {\displaystyle w(x)} $w(x)$ popisuje průhyb nosníku ve $z$ směru z {\displaystyle z} v určité poloze x {\displaystyle x} . q {\displaystyle q} je rozložené zatížení, jinými slovy síla na jednotku délky (obdobně jako tlak je síla na plochu); může být funkcí x {\displaystyle x} , w {\displaystyle w}. $w$ nebo jiné proměnné.

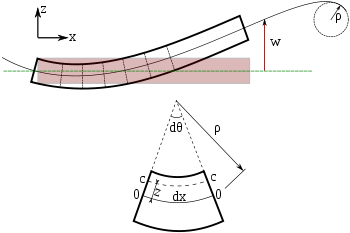
Ohyb Eulerova-Bernoulliho nosníku. Každý průřez nosníku je v úhlu 90 stupňů k neutrální ose.

Otázky a odpovědi

Otázka: Co je to Eulerova-Bernoulliho teorie paprsků?

Odpověď: Eulerova-Bernoulliho teorie nosníků je jednoduchá metoda používaná k výpočtu ohybu nosníků při zatížení bez uvažování účinků smykových deformací.

Otázka: Kdy byla poprvé zavedena Eulerova-Bernoulliho teorie nosníků?

Odpověď: Eulerova-Bernoulliho teorie nosníků byla poprvé zavedena kolem roku 1750.

Otázka: Byla Eulerova-Bernoulliho teorie nosníků použita při vývoji Eiffelovy věže a ruského kola?

Odpověď: Ano, Eulerova-Bernoulliho teorie paprsků se stala populární při vývoji Eiffelovy věže a ruského kola na konci 19. století.

Otázka: V jakých technických oborech se Eulerova-Bernoulliho teorie nosníků uplatnila?

Odpověď: Eulerova-Bernoulliho teorie nosníků byla použita v mnoha technických oborech včetně strojírenství a stavebnictví.

Otázka: Používá se Eulerova-Bernoulliho teorie nosníků ještě dnes?

Odpověď: Ano, Eulerova-Bernoulliho teorie nosníku se dnes stále hojně používá pro svou jednoduchost, i když byly vyvinuty jiné pokročilé metody.

Otázka: Pro jaké typy průhybů nosníku platí Eulerova-Bernoulliho teorie nosníku?

Odpověď: Eulerova-Bernoulliho teorie nosníku platí pro malé výchylky nosníku.

Otázka: Bere Eulerova-Bernoulliho teorie nosníku v úvahu účinky smykových deformací?

Odpověď: Ne, Eulerova-Bernoulliho teorie nosníku nezohledňuje účinky smykových deformací.