Pravidlo pravé ruky
Pravidlo pravé ruky je konvence ve vektorové matematice. Pomáhá vám zapamatovat si směr, když se vektory křížem násobí.
1. Začněte tím, že zavřete pravou ruku a vystrčte ukazováček.
2. Vztyčte palec, jako byste dělali znamení pro zbraň.
3. Pokud míříte přímo před sebe, vystrčte prostředníček tak, aby směřoval doleva a všechny prsty svíraly navzájem pravý úhel.
Pokud máte dva vektory, které chcete vynásobit křížem, můžete směr vektoru, který z nich vyjde, zjistit tak, že palcem ukážete ve směru prvního vektoru a ukazovátkem ve směru druhého vektoru. Prostředníček bude ukazovat směr křížového součinu.
Nezapomeňte, že když změníte pořadí křížového násobení vektorů, výsledek se změní v opačném směru. Proto je důležité dbát na to, abyste postupovali v pořadí t h u m b → × p o i n t e r → = m i d l e → {\displaystyle {\vec {thumb}}\times {\vec {pointer}}={\vec {middle}}}. 
.
Pravidlo pravé ruky pro pohyb vyvolaný šroubovými závity
Vlevo je zobrazena orientace pro leváky, vpravo pro praváky.
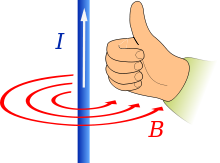
Předpověď směru pole (B), když proud I teče ve směru palce
Varianty
Existuje ještě jedno pravidlo, které se nazývá pravidlo pravé ruky (nebo pravidlo vývrtky) a používá se pro magnetická pole a věci, které se otáčejí.
1. Začněte tím, že pravou ruku natáhnete naplocho a palec nasměrujete rovně tak, aby svíral pravý úhel s ostatními prsty.
2. Nyní zatněte prsty v pěst a palec nechte venku (jako palec nahoru).
3. Přizpůsobte své prsty tomu, jak se něco pohybuje. Směr, kterým ukazuje palec, je směrem vektoru, který používáme, když o něm mluvíme.
Můžete to udělat i obráceně - začněte palcem ve směru vektoru a sledujte, jak se vám kroutí prsty, abyste zjistili směr otáčení. Pokud namíříte palec ve směru proudu ve vodiči, magnetické pole, které se kolem něj vytvoří, je ve směru kroucení vašich prstů.
Otázky a odpovědi
Otázka: Co je to pravidlo pravé ruky?
Odpověď: Pravidlo pravé ruky je konvence ve vektorové matematice, která pomáhá zapamatovat si směr, když se vektory křížem násobí.
Otázka: Jak se používá pravidlo pravé ruky k určení směru křížového součinu?
Odpověď: Chcete-li zjistit směr křížového součinu, zavřete pravou ruku a vystrčte ukazováček. Palec vystrčte přímo nahoru, jako byste dělali znamení pro zbraň. Namířte "zbraň" přímo před sebe a pak vystrčte prostředníček tak, aby ukazoval doleva a všechny prsty svíraly navzájem pravý úhel. Ukažte palcem ve směru prvního vektoru a ukazovákem ve směru druhého vektoru. Váš prostředníček bude ukazovat ve směru křížového součinu.
Otázka: Co se stane, když při křížovém násobení vektorů změníte pořadí?
Odpověď: Když při křížovém násobení vektorů změníte pořadí, výsledek půjde opačným směrem. Proto je důležité dbát na to, abyste postupovali v pořadí palec x ukazovák = prostředník .
Otázka: Co znamená tato rovnice? {\displaystyle {\vec {palec}}\krát {\vec {ukazatel}}={\vec {střed}}} .
Odpověď: Tato rovnice znamená, že pokud se dva vektory vzájemně vynásobí (palec x ukazatel), vznikne třetí vektor (middle).
