Paralaxa
Paralaxa je vnímaná změna polohy objektu při pohledu ze dvou různých míst.
V astronomii je roční paralaxa jediným přímým způsobem měření vzdálenosti hvězd mimo sluneční soustavu. Paralaxa je v podstatě vnímaný jev posunu, ke kterému dochází při pohledu na objekt z různých pozic.
Měří se pomocí úhlu mezi dvěma pozorovacími přímkami. Blízké objekty mají při pozorování ze stejných pozic větší paralaxu než objekty vzdálenější, takže paralaxu lze použít k určení vzdáleností.
Astronomové používají princip paralaxy k měření vzdáleností nebeských objektů včetně Měsíce, Slunce a hvězd mimo Sluneční soustavu. Pojem "paralaxa" zde představuje úhel mezi dvěma přímkami pohledu na hvězdu.
Astronomická měření polohy se provádějí v různých ročních obdobích. Protože je přesně známa dráha Země, lze vypočítat vzdálenost z polohy 1 do polohy 2. Úhel od obzoru k objektu lze změřit přesně. Tím získáme trojúhelník, jehož základna a úhly jsou přesně známy. Z trojúhelníku se pomocí trigonometrie vypočítá vzdálenost a vyjádří se v parsecích.
Metoda selhává pouze u objektů, které jsou natolik vzdálené, že dráha Země je příliš malá na to, aby bylo možné získat dostatečně velký úhel paralaxy pro přesné měření. Tato vzdálenost je asi 100 světelných let. Astronomové vymysleli různé způsoby, jak tento problém vyřešit, žádný z nich však není tak přesný jako metoda paralaxy pro relativně blízké objekty. To poskytuje základ pro žebříček kosmických vzdáleností technik pro výpočet větších vzdáleností.
V letech 1989 až 1993 provedla družice Hipparcos měření u více než 100 000 blízkých hvězd. Gaia (kosmická sonda) má provést podobná měření u přibližně miliardy hvězd.
Mnoho živočichů, včetně lidí, má dvě oči, které umožňují vnímání hloubky; tomu se říká stereopse. Protože se obě oči nacházejí na různých místech hlavy, je to základ pro automatické vnímání vzdálenosti. Vnímáme ji jako běžnou trojrozměrnou scénu.
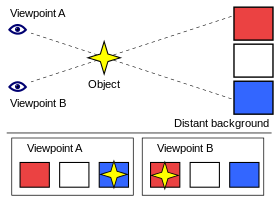
Příklad paralaxy objektu na vzdáleném pozadí v důsledku změny polohy. Při pohledu z "bodu A" se zdá, že objekt je před modrým čtvercem. Při změně úhlu pohledu na "Úhel pohledu B" se zdá, že se objekt přesunul před červený čtverec.
Otázky a odpovědi
Otázka: Co je to paralaxa?
Odpověď: Paralaxa je vnímaná změna polohy objektu při pohledu ze dvou různých míst. Měří se pomocí úhlu mezi dvěma pozorovacími přímkami a lze ji použít k určení vzdáleností.
Otázka: Jak se paralaxa používá v astronomii?
Odpověď: V astronomii je roční paralaxa jediným přímým způsobem měření vzdálenosti hvězd mimo sluneční soustavu. Astronomové používají princip paralaxy k měření vzdáleností nebeských objektů včetně Měsíce, Slunce a hvězd mimo sluneční soustavu.
Otázka: Jak se počítá vzdálenost pomocí paralaxy?
Odpověď: Astronomická měření polohy se provádějí v různých ročních obdobích. Jelikož je dráha Země přesně známa, lze vypočítat vzdálenost z polohy 1 do polohy 2. V tomto případě je možné použít paralaxu. Lze přesně změřit úhel od obzoru k objektu, čímž získáme trojúhelník, jehož základna a úhly jsou přesně známy. Z tohoto trojúhelníku lze pomocí trigonometrie vypočítat vzdálenosti vyjádřené v parsecích.
Otázka: Existují nějaká omezení při použití paralaxy pro měření vzdálených objektů?
Odpověď: Ano, selhává u objektů, které jsou tak vzdálené, že oběžná dráha Země je příliš malá na to, aby byl úhel paralaxy dostatečně velký pro přesné měření - asi 100 světelných let a více. Byly vynalezeny i jiné metody, ale žádná není tak přesná jako paralaxa pro relativně blízké objekty.
Otázka: Jaká družice byla v letech 1989-1993 používána pro měření blízkých hvězd?
Odpověď: V tomto období byla použita družice Hipparcos, která provedla měření více než 100 000 blízkých hvězd.
Otázka: Jaká sonda bude provádět podobná měření jako Hipparcos? O: Gaia (kosmická sonda) bude provádět podobná měření asi miliardy hvězd.
Vyhledávání