Hollandova věta o schématu

Popis

Uvažujme binární řetězce délky 6. Schéma 1*10*1 popisuje množinu všech řetězců délky 6 s jedničkami na pozicích 1, 3 a 6 a nulou na pozici 4. Znak * je zástupný symbol, což znamená, že pozice 2 a 5 mohou mít hodnotu 1 nebo 0. Pořadí schématu o ( H ) {\displaystyle o(H)} je definováno jako počet pevných pozic v šabloně, zatímco definiční délka δ ( H ) {\displaystyle \delta (H)} je vzdálenost mezi první a poslední konkrétní pozicí. Řád 1*10*1 je 4 a jeho definiční délka je 5. Fitness schématu je průměrná fitness všech řetězců odpovídajících schématu. Fitness řetězce je mírou hodnoty zakódovaného řešení problému vypočtené vyhodnocovací funkcí specifickou pro daný problém. S využitím zavedených metod a genetických operátorů genetických algoritmů věta o schématu říká, že krátká schémata nízkého řádu s nadprůměrnou fitness v následujících generacích exponenciálně rostou. Vyjádřeno rovnicí:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1 - p]. }

Zde m ( H , t ) {\displaystyle m(H,t)} je počet řetězců patřících do schématu H {\displaystyle H} v generaci t {\displaystyle t}. , f ( H ) {\displaystyle f(H)} je pozorovaná průměrná fitness schématu H {\displaystyle H} a a t {\displaystyle a_{t}} je pozorovaná průměrná fitness v generaci t {\displaystyle t} . Pravděpodobnost narušení p {\displaystyle p} je pravděpodobnost, že křížení nebo mutace zničí schéma H {\displaystyle H} . Lze ji vyjádřit jako:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}}

kde o ( H ) {\displaystyle o(H)} je pořadí schématu, l {\displaystyle l} je délka kódu, p m {\displaystyle p_{m}} je pravděpodobnost mutace a p c {\displaystyle p_{c}} je pravděpodobnost křížení. Schéma s kratší definiční délkou δ ( H ) {\displaystyle \delta (H)} má tedy menší pravděpodobnost narušení.
Často nepochopeným bodem je, proč je věta o schématu nerovností, a nikoli rovností. Odpověď je ve skutečnosti jednoduchá: Věta zanedbává malou, ale nenulovou pravděpodobnost, že řetězec patřící do schématu H {\displaystyle H} vznikne "od nuly" mutací jednoho řetězce (nebo rekombinací dvou řetězců), který v předchozí generaci nepatřil do H {\displaystyle H} .

Omezení

Věta o schématech platí za předpokladu genetického algoritmu, který udržuje nekonečně velkou populaci, ale ne vždy se přenáší do (konečné) praxe: v důsledku chyby výběru vzorků v počáteční populaci mohou genetické algoritmy konvergovat ke schématům, která nemají žádnou selekční výhodu. K tomu dochází zejména v multimodální optimalizaci, kde funkce může mít více vrcholů: populace může driftovat tak, že bude preferovat jeden z vrcholů a ignorovat ostatní.

Důvodem, proč věta o schématu nemůže vysvětlit sílu genetických algoritmů, je to, že platí pro všechny případy problémů a nedokáže rozlišit mezi problémy, ve kterých genetické algoritmy fungují špatně, a problémy, ve kterých genetické algoritmy fungují dobře.

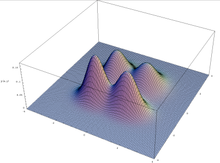
Graf multimodální funkce ve dvou proměnných.