Problém s rozhodnutím
V teorii vypočitatelnosti a teorii výpočetní složitosti je rozhodovací problém otázka v nějakém formálním systému s odpovědí ano nebo ne. Odpověď závisí na hodnotách vstupních parametrů. Rozhodovací problémy se typicky objevují v matematických otázkách rozhodnutelnosti, tj. v otázce existence efektivní metody pro určení existence nějakého objektu nebo jeho příslušnosti k množině. Některé z nejdůležitějších problémů v matematice jsou nerozhodnutelné.
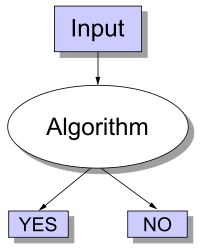
Rozhodovací problém má pouze dva možné výstupy, ano nebo ne (nebo střídavě 1 nebo 0) na každém vstupu.
Otázky a odpovědi
Otázka: Co je to rozhodovací problém?
Odpověď: Rozhodovací problém je otázka v nějaké formální soustavě s odpovědí ano nebo ne, která závisí na hodnotách vstupních parametrů.
Otázka: V jakých oborech se vyskytují rozhodovací problémy?
A: Rozhodovací problémy se obvykle objevují v matematických otázkách rozhodovatelnosti.
Otázka: Jaký je význam rozhodovatelnosti?
Odpověď: Rozhodnutelnost se týká otázky existence efektivní metody, jak určit existenci nějakého objektu nebo jeho příslušnost k množině.
Otázka: Jsou všechny problémy v matematice rozhodnutelné?
Odpověď: Ne, některé z nejdůležitějších problémů v matematice jsou nerozhodnutelné.
Otázka: Co je nerozhodnutelný problém?
Odpověď: Nerozhodnutelný problém je problém, pro který neexistuje algoritmus, který by vždy poskytl odpověď ano nebo ne v konečném čase.
Otázka: Je odpověď na rozhodovací problém vždy ano nebo ne?
Odpověď: Ano, odpověď na rozhodovací problém je vždy ano nebo ne.
Otázka: Na čem závisí odpověď na rozhodovací problém?
Odpověď: Odpověď na rozhodovací problém závisí na hodnotách vstupních parametrů.
Vyhledávání